Question: Let X be a random variable taking on n values with probabilities p1, p2, . . . , pn. Recall from Lecture 9 that the

Let X be a random variable taking on n values with probabilities p1, p2, . . . , pn. Recall from Lecture 9 that the min-entropy of X, denoted E(X), is given by

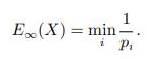
Let X be a random variable taking on n values with probabilities

If X is uniformly distributed then p1 = p2 = = pn = 1 .

(a) Show that if X is not uniformly distributed then necessarily one of the pi s is > 1.

(b) Show that if X is not uniformly distributed then E(X)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Let X be a random variable taking on values a1, a2, . . . , pr with probabilities p1, p2, . . . , pr and with E(X) = μ. Define the spread of X as follows: This, like the standard deviation, is a...

Detailed answers. Problem 34.\" A spider and a y move along a straight line. At each second, the y moves a unit step to the right or to the left with equal probability p, and stays where it is with...

As for the code you can only answer 1 question, so please answer question 2. PROBLEM B: Alpha is deciding whether to invest $1,000 in a mutual fund. In one year, the mutual fund gives a return of 20%...

10/29/2015 Week 6 Assignment YINWEI LIU CED 6030, section 02, Fall 2015 Instructor: He Wang WebAssign Week 6 Assignment (Homework) Current Score : - / 114 Due : Wednesday, November 4 2015 11:59 PM...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

GIVE DETAILED WORKING IN ALL QUESTIONS. Suppose that a game is to be played with a single die assumed fair. In this game a player wins $20 if a 2 turns up, $40 if a 4 turns up; loses $30 if a 6 turns...

"10 A natural ancillary statistic In most problems is the sample size . For example , let IN` he a random variable taking values 1 , 2 . ... with known probabilities p1 , p2 . .... where I'D; = 1 ....

How do find these values with the Z table. Part 3: Estimating Probability Next, we will look more into the standard normal curve and what percentiles and probabilities are associated with the...

FNB results show double digit growth as digital strategy takes off (Bloomberg) You wouldnt say South Africa was in the grips of a recession by looking at the retail-banking unit of FirstRand Ltd.,...

When will silence be considered an acceptance of an offer?

A current liability is slways a short - term obligation expected to ne paid within one year of the balance sheet date. True or false?

Required information Trey Monson starts a merchandising business on December 1 and enters into the following three inventory purchases Also, on December 15, Monson sells 30 units for $35 each...

4. Competition in quality and service may be just as effective as price competition in giving buyers more for their money. Do you agree? Why? Explain why monopolistically competitive firms frequently...

LO13.3 Explain why monopolistic competition delivers neither productive nor allocative efficiency.

3. Monopolistic competition is monopolistic up to the point at which consumers become willing to buy close substitute products and competitive beyond that point. Explain. LO13.2