Question: Let (x): R R be a non-negative function, so that f(x)dx = 1. Show that for any continuous function f : RR, we have

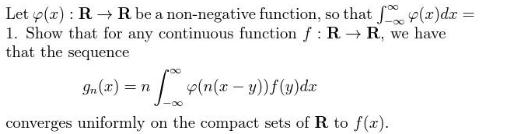
Let (x): R R be a non-negative function, so that f(x)dx = 1. Show that for any continuous function f : RR, we have that the sequence In(x) = n (n(x-y))f(y)dx converges uniformly on the compact sets of R to f(x).

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Gary would like to invest in gold and is aware that the returns on such an investment can be quite volatile. Use the following table of states, probabilities, and returns to determine the coefficient...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Jonfreningar r i regel... (ett alternativ r korrekt) 1. vtskor med hg kokpunkt 2. fasta mnen med lg smltpunkt 3. fasta mnen med hg smltpunkt 4. vtskor med lg kokpunkt 5. gasformiga mnen

Find the density of X + 1 2Y . Is it the same as the density of max{X, Y}? (Cambridge 2007) 25. Let X and Y have the bivariate normal density function f (x, y) = 1 2 p 1 2 exp 1 2(1 2) (x2 2xy +...

Bamboo Consulting End-of-Period Spreadsheet For the Year Ended July 31, 20Y5 Unadjusted Adjusted Trial Balance Adjustments Trial Balance Account Title Dr. Cr. Dr. Cr. Dr. Cr. Cash 11,100 11,100...

1. Kim Co. purchased goods with a list price of $175,000, subject to trade discounts of 20% and 10%, with no cash discounts allowable. How much should Kim Co. record as the cost of these goods? 2....

solve this question Problem 3 Let X1. .... X, be independent and identically distributed continuous random variables with a positive continuous joint probability density function f(x1. . . ., X'n)....

Problem 3 Let X1. .... X, be independent and identically distributed continuous random variables with a positive continuous joint probability density function f(x1. . . ., X'n). 3pts (i) Suppose that...

Financial Statements of a Manufacturing Firm The following events took place for Focault Inc. during July 20Y2, the first month of operations as a producer of road bikes: . . Purchased $365,400 of...

for which of the following decisions is vendor reputation a major qualitative question? a) constrained capacity b) special order c) outsourcing also know as make vs buy d) international

The given multivariable function is as follows: f ( x , y ) = ky 2 - 2 y 3 - kx 3 + 2 kxy . A. Given that the function f ( x,y ) in the Assumptions section has a critical point at (0,0), use a second...

How often should braille accommodations be provided? A. Never, not enough people use it. B. Always, regardless of how many people use it. C. Sometimes if it was requested by someone who needs it. D....

Refer to the information in question. In question, The Woods Enterprises prepared the following standard costs for the production of one stuffed bear: Direct materials..... 1.5 pounds of stuffing @...

The following events apply to Montgomery Company for 2016, its first year of operation: 1. Received cash of $36,000 from the issue of common stock. 2. Performed $48,000 of services on account. 3....

Ryan Company reports net income of $5,125 for the year ended December 31, 2007, its first year of operations. On January 3, 2007, the company issued 9,000 shares of common stock . On August 1, 2007...

Hector Company has developed the following standard costs for its product for 2012: HECTOR COMPANY Standard Cost Card Product A Cost Element...... Standard Quantity...... Standard Price .....=...

Mix a concoction of 10 percent 7-Up or Sprite (or similar clear beverage) and 90 percent apple juice. Have two different consumers try the concoction. For one, ask them to try this new soft drink....

A firm has total assets of $ 1 0 0 and total debt of $ 2 5 . Equity is $ 7 5 . Debt - equity ratio is 3 . Debt ratios is 2 5 % . Equity ratio is 7 5 % .

The uniform distribution on the interval [, + 3], where the value of is unknown (

Consider again the conditions of Exercise 19, and let denote the M.L.E. of . a. Use the delta method to determine the asymptotic distribution of 1/. b. Show that 1/ = n, and use the central limit...

Find the mode of the 2 distribution with m degrees of freedom (m = 1, 2, . . .).

17. What is an example of an unconscious visually guided behavior?

12. If light strikes only one receptor, what is the net eff ect (excitatory or inhibitory) on the nearest bipolar cell that is directly connected to that receptor? What is the eff ect on bipolar...

13. Examine Figure 6.17. You should see grayish diamonds at the crossroads among the black squares. Explain why.