Let Yt be a process such that, for Vt

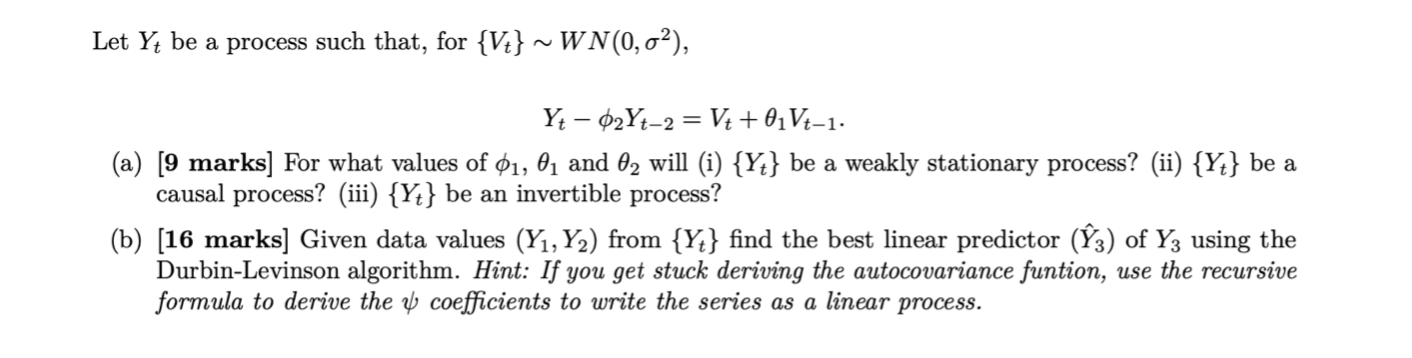
Let Yt be a process such that, for {Vi} ~ WN(0, 62), Yt - $2 Yt-2 = V+ + 01Vt-1. (a) [9 marks] For what values of 1, 01 and 02 will (i) {Yt} be a weakly stationary process? (ii) {Yt} be a causal process? (iii) {Yt} be an invertible process? (b) [16 marks] Given data values (Y1, Y2) from {Yt} find the best linear predictor (Y3) of Y3 using the Durbin-Levinson algorithm. Hint: If you get stuck deriving the autocovariance funtion, use the recursive formula to derive the y coefficients to write the series as a linear process