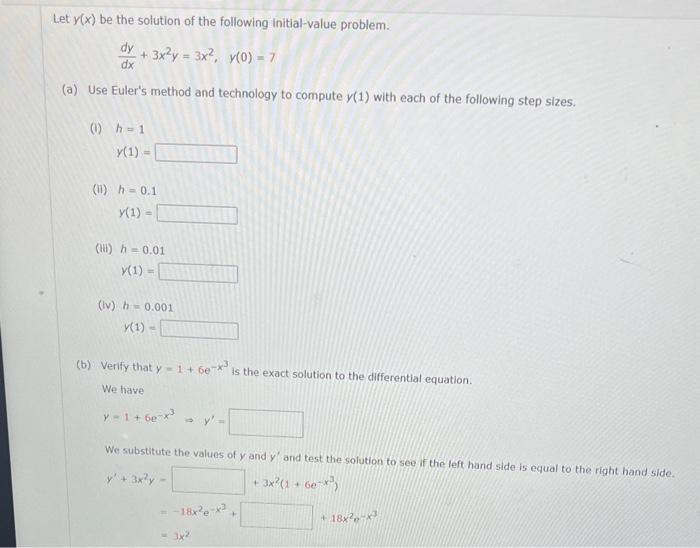
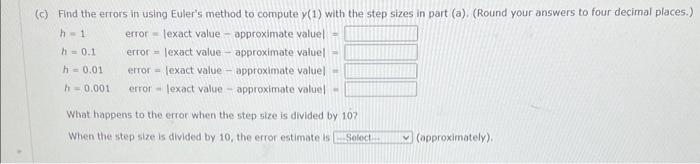
Question: Let y(x) be the solution of the following initial-value problem. dxdy+3x2y=3x2,y(0)=7 (a) Use Euler's method and technology to compute y(1) with each of the following
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


