Lets continue working on the ant tunnel-building question you started in the previous assignment: How long does it take an ant to build a tunnel? Heres a reminder of the setup from Part 1: Let x be the length of the tunnel in feet that an ant builds. Let T(x) be the time in hours it takes the ant to build the tunnel of length x. We can get some idea of our situation by making a sketch.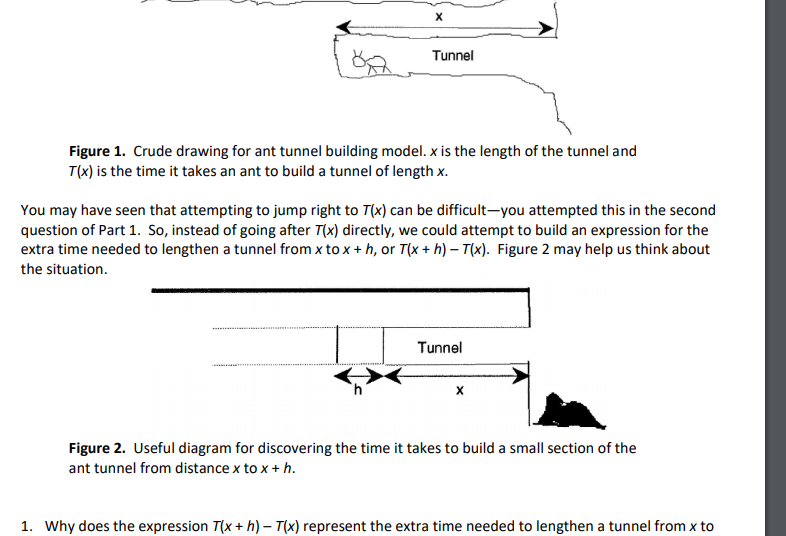

1. Why does the expression T(x + h) T(x) represent the extra time needed to lengthen a tunnel from x to x + h? What are some assumptions which (a) reflect the reality of this scenario and (b) might make the model simpler in a first attempt? 2 Now lets see if we can build a model using these assumptions to help us determine how long it might take an ant to extend a tunnel from distance x to distance x + h. Thus, we seek an expression for T(x + h) T(x). Notice that T(x + h) T(x) T(h), since T(h) represents the time it takes to dig a small tunnel of length h from the mouth of the tunnel, while T(x + h) T(x) includes the time it takes to extend the tunnel from length x to x + h. This latter time must account for the time for the ant to bring the material all the way out along a path of length x from the region from x to x + h, which is more than just the time it takes, T(h), to bring the material a distance of only h to the mouth of the tunnel.

2. List the variables (present or to be introduced) and parameters (constants) on which the expression in T(x + h) T(x) might depend.

3. Below are several possible mathematical models for T(x + h) T(x). Where they appear, a, b, and c are positive real constants (parameters). Defend or reject each and offer your reasons. Perhaps modify several of them and make them better or add your own models. When trying to reject a model consider some trivial cases and see if the model makes sense, for example h = 0 or x = 0 or either h or x very large. a. T(x + h) T(x) = ax + bh b. T(x + h) T(x) = ax bh c. T(x + h) T(x) = axbh d. T(x + h) T(x) = axh e. T(x + h) T(x) = bhax f. T(x + h) T(x) = c

4. For the models in 3 that make sense, what could a, b, and c represent?

Tunnel Figure 1. Crude drawing for ant tunnel building model. x is the length of the tunnel and T(x) is the time it takes an ant to build a tunnel of length x. You may have seen that attempting to jump right to Tx) can be difficult-you attempted this in the second question of Part 1. So, instead of going after T(x) directly, we could attempt to build an expression for the extra time needed to lengthen a tunnel from xto x + h, or T(x + h) - T(x). Figure 2 may help us think about the situation. Tunnel Figure 2. Useful diagram for discovering the time it takes to build a small section of the ant tunnel from distance x to x + h. 1. Why does the expression T(x + h) - T(x) represent the extra time needed to lengthen a tunnel from x to Tunnel Figure 1. Crude drawing for ant tunnel building model. x is the length of the tunnel and T(x) is the time it takes an ant to build a tunnel of length x. You may have seen that attempting to jump right to Tx) can be difficult-you attempted this in the second question of Part 1. So, instead of going after T(x) directly, we could attempt to build an expression for the extra time needed to lengthen a tunnel from xto x + h, or T(x + h) - T(x). Figure 2 may help us think about the situation. Tunnel Figure 2. Useful diagram for discovering the time it takes to build a small section of the ant tunnel from distance x to x + h. 1. Why does the expression T(x + h) - T(x) represent the extra time needed to lengthen a tunnel from x to