Linear Algebra

Final answer only - No Explanation

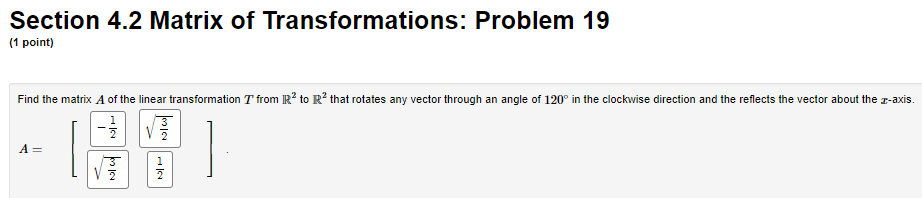
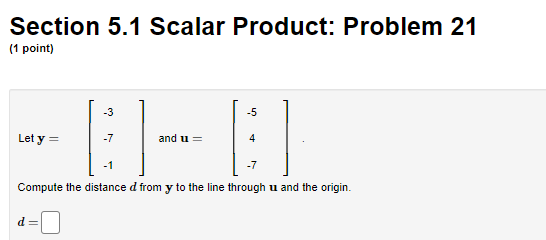
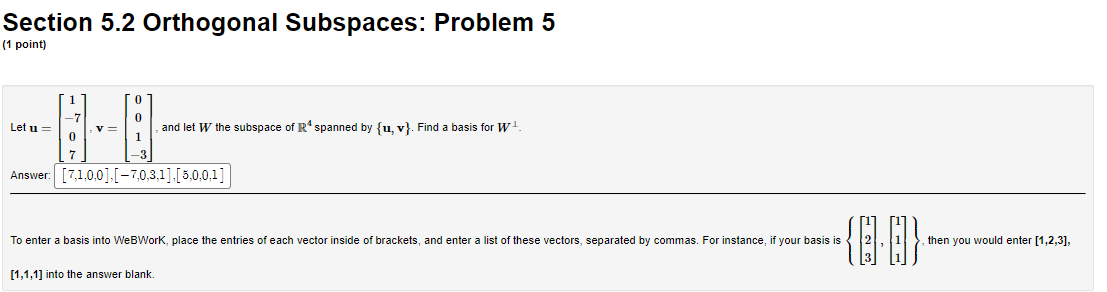
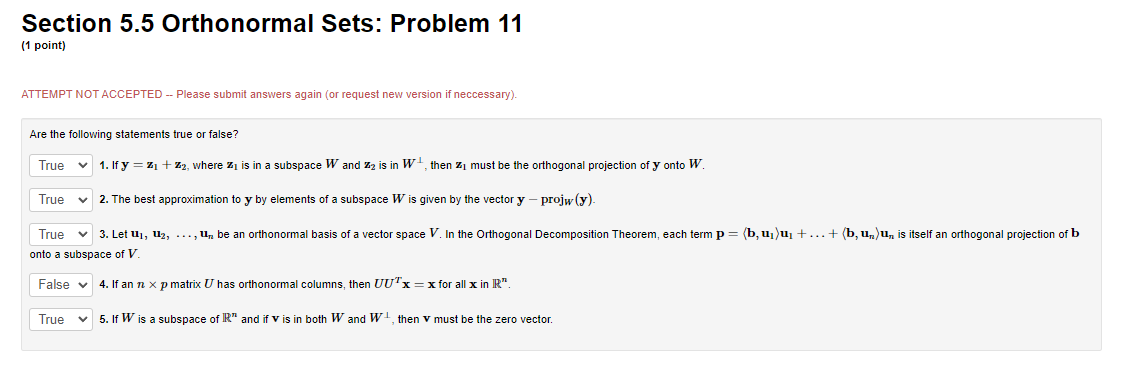
Section 4.2 Matrix of Transformations: Problem 7 :1 point: Find the malrix A of the linear transformation T from lit\" to R2 that rotates any 'Jectorthrough an angle oi {50\" in the counterclockwise direction Section 4.2 Matrix of Transformations: Problem 16 (1 point) Find the matrix A of the linear transformation 7' from IR to R' that rotates any vector through an angle of 150" in the clockwise direction A =Section 4.2 Matrix of Transformations: Problem 19 (1 point) Find the matrix A of the linear transformation 7' from IR to R that rotates any vector through an angle of 120" in the clockwise direction and the reflects the vector about the r-axis. A =Section 5.1 Scalar Product: Problem 6 (1 point) 2 Let x = Find the norm of x and the unit vector in the direction of x. 2 -2 4 1 = 2 -4Section 5.1 Scalar Product: Problem 19 :1 point: Find the distance from the point {B 3] to the line 3:: 4y : n a: Distance = v? Section 5.1 Scalar Product: Problem 21 (1 point) -5 Let y = -7 and 11 = 4 Compute the distance d from y to the line through u and the origin. d=Section 5.2 Orthogonal Subspaces: Problem 3 (1 point) Let L be the line spanned by 5 in IR'S. Find a basis of the orthogonal complement _ of L. Answer: [5,1.0],[-8,0,1] To enter a basis into WeBWork, place the entries of each vector inside of brackets, and enter a list of these vectors, separated by commas. For instance, if your basis is then you would enter [1,2,3], [1,1,1] into the answer blank.Section 5.2 Orthogonal Subspaces: Problem 5 (1 point) Let u = and let W the subspace of R spanned by {u, v}. Find a basis for W L. Answer: [7,1,0,0],[-7,0,3,1],[ 5,0,0,1 ] To enter a basis into WeBWork, place the entries of each vector inside of brackets, and enter a list of these vectors, separated by commas. For instance, if your basis is then you would enter [1,2,3], [1,1,1] into the answer blank.Section 5.5 Orthonormal Sets: Problem 11 (1 point) ATTEMPT NOT ACCEPTED -- Please submit answers again (or request new version if necessary). Are the following statements true or false? True v 1. If y = 21 + %2, where 21 is in a subspace W and %2 is in W, then 21 must be the orthogonal projection of y onto W. True v 2. The best approximation to y by elements of a subspace W is given by the vector y - projw (y)- True 3. Let U], U2, ..., Un be an orthonormal basis of a vector space V. In the Orthogonal Decomposition Theorem, each term p = (b, uj)uj + ... + (b, Un)Un is itself an orthogonal projection of b onto a subspace of V. False v 4. If an n x p matrix U has orthonormal columns, then UUx = x for all x in IR". True v 5. If W is a subspace of IR" and if V is in both W and W, then v must be the zero vector.Section 5.5 Orthonormal Sets: Problem 12 (1 point) 0.5 -0.5 0.5 -0.5 Let A = . Note that the columns of A are orthonormal (why?). 0.5 0.5 0.5 0.5 (a) Solve the least squares problem Ax = b where b = * = (b) Find the projection matrix P that projects vectors in R* onto R(A) 0000 10OO P = (c) Compute Ax and Pb Ax = Pb =