Linear algebra mathlab

MATLAB code for performing the calculation,

an explanation of how to interpret the output from MATLAB to give an answer to the original question.

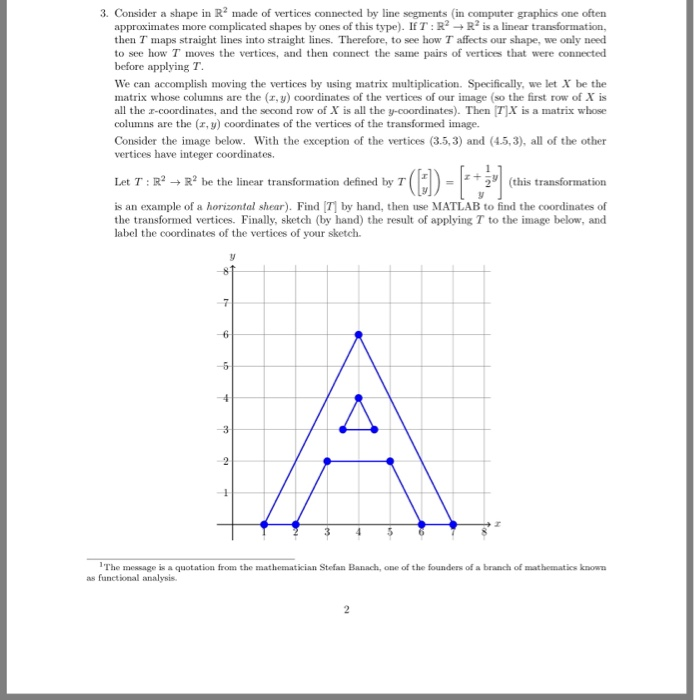
3. Consider a shape in R2 made of vertices connected by line segments (in computer graphics one often approximates more complicated shapes by ones of this type). IT:R2R2 is a linear transformation, then T maps straight lines into straight lines. Therefore, to see how T affects our shape, we only need to see how T moves the vertices, and then connect the same pairs of vertices that were connected before applying T We can accomplish moving the vertices by using matrix multiplication. Specifically, we let X be the matrix whose columns are the (r, y) coordinates of the vertices of our image (so the first row of X is all the z-coordinates, and the second row of X is all the y-coordinates). Then TIX is a matrix whose columns are the (x,y) coordinates of the vertices of the transformed image. Consider the image below. With the exception of the vertices (3.5,3) and (45,3), all of the other vertices have integer coordinates. Let T : R2 R2 be the linear transformation defined by TUED-1 21 (this transformation is an example of a horizontal shear). Find T by hand, then use MATLAB to find the coordinates of the transformed vertices. Finally, sketch (by hand) the result of applying T to the image below, and label the coordinates of the vertices of your sketch -8 The message is a quotation from the mathomatician Stefan Banach, one of the founders of a branch of mathmatics kno as functional analysis 3. Consider a shape in R2 made of vertices connected by line segments (in computer graphics one often approximates more complicated shapes by ones of this type). IT:R2R2 is a linear transformation, then T maps straight lines into straight lines. Therefore, to see how T affects our shape, we only need to see how T moves the vertices, and then connect the same pairs of vertices that were connected before applying T We can accomplish moving the vertices by using matrix multiplication. Specifically, we let X be the matrix whose columns are the (r, y) coordinates of the vertices of our image (so the first row of X is all the z-coordinates, and the second row of X is all the y-coordinates). Then TIX is a matrix whose columns are the (x,y) coordinates of the vertices of the transformed image. Consider the image below. With the exception of the vertices (3.5,3) and (45,3), all of the other vertices have integer coordinates. Let T : R2 R2 be the linear transformation defined by TUED-1 21 (this transformation is an example of a horizontal shear). Find T by hand, then use MATLAB to find the coordinates of the transformed vertices. Finally, sketch (by hand) the result of applying T to the image below, and label the coordinates of the vertices of your sketch -8 The message is a quotation from the mathomatician Stefan Banach, one of the founders of a branch of mathmatics kno as functional analysis