Question: Linear Programming: Lesson in Excel (using solver) or Lindo Transshipment Model: This is an extension of the transportation model. There are now intermediate transshipment points

Linear Programming:

Lesson in Excel (using solver) or Lindo

Transshipment Model: This is an extension of the transportation model. There are now intermediate transshipment points added between the sources (plants) and destinations (retailers). Items being shipped from a Plant (p_i) must be shipped to a Warehouse (w_j) before being shipped to the Retailer (r_k). Each Plant will have an associated supply (s_i) and each Retailer will have a demand (d_k). The number of plants is n, number of warehouses is q and the number of retailers is m. The edges (i,j) from plant (p_i)to warehouse (w_j) have costs associated denoted cp(i,j). The edges (j,k) from a warehouse (w_j)to a retailer (r_k) have costs associated denoted cw(j,k). The graph below shows the transshipment map for a manufacturer of refrigerators. Refrigerators are produced at four plants and then shipped to a warehouse (weekly) before going to the retailer.

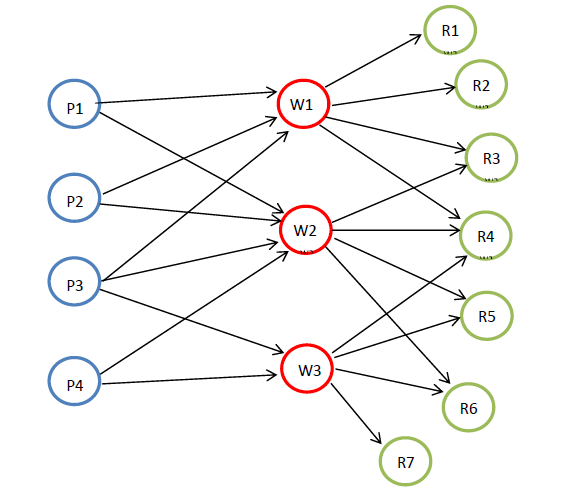
Linear Programming: Lesson in Excel (using solver) or Lindo Transshipment Model: This

Below are the costs of shipping from a plant to a warehouse and then a warehouse to a retailer. If it is impossible to ship between the two locations an X is placed in the table.

cost	W1	W2	W3
P1	$10	$15	X
P2	$11	$8	X
P3	$13	$8	$9
P4	X	$14	8

cost	R1	R2	R3	R4	R5	R6	R7
W1	$5	$6	$7	$10	X	X	X
W2	X	X	$12	$8	$10	$14	X
W3	X	X	X	$14	$12	$12	$6

	P1	P2	P3	P4
Supply	150	450	250	150

	R1	R2	R3	R4	R5	R6	R7
Demand	100	150	100	200	200	150	100

Lesson in Excel (using Solver) or Lindo

Part 1: The optimal shipping routes and minimum cost is $17100 but due to old infrastructure Warehouse 2 is going to close eliminating all of the associated routes. What is the optimal solution for this modified model? Is it feasible to ship all the refrigerators to either warehouse 1 or 3 and then to the retailers without using warehouse 2? Why or why not?

Part 2: Instead of closing Warehouse 2 management has decide to keep a portion of it open but limit shipments to 100 refrigerators per week. Is this feasible? If so what is the optimal solution when warehouse 2 is limited to 100 refrigerators?

R1 R2 P1 W1 P2 P3 R5 R6 R7 R1 R2 P1 W1 P2 P3 R5 R6 R7

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Linear Programming: Lesson in Excel (using solver) or Lindo Transshipment Model: This is an extension of the transportation model. There are now intermediate transshipment points added between the...

Transshipment Model: This is an extension of the transportation model. There are now intermediate transshipment points added between the sources (plants) and destinations (retailers). Items being...

I've solved the first 3 parts of the problem. I need help with the last part at the very bottom. For this problem I am using lindo as below..... THE QUESTION I NEED HELP WITH IS: Instead of closing...

You may solve the problems using your choice of software, state which software package/language(s) you used and provide the code or spreadsheet. Can this be done with a spreadsheet? I would prefer...

Please refer to the Zeron Case of Transshipment Problem which is attached below. Please set up the linear program in Excel and solve it by using Excel Solver according to the LP formulation. Please...

Rename the Excel file in the following way: Lastname_firstname_AGEC 3413_Fall 22_HW 4" while submitting. For question # 2 you need to use a word file. The word file should be named in the following...

Here is the new homework question. Please review the General Homework instructions due to the instructor being so strict. Were there any podcasts or Homework document notes that you needed me to...

need problem 43 and 45 pls and thank you 43. Consider Example 7.7 of the Pear Company assuming the following supplies and demands. Use Excel's Solver (or other linear programming code) to determine...

This is an extension of the transportation model. . There are now intermediate transshipment points added between the sources (plants) and destinations (retailers). Items being shipped from a Plant...

3. Transshipment Model (10 points) This is an extension of the transportation model. There are now intermediate transshipment points added between the sources (plants) and destinations (retailers)....

Sketch roughly the magnitude |X (?)| of the Fourier transforms corresponding to the pole-zero patterns given in figure. Unit circle Douhle pole Pole at 0.9" Linit circle Double zero th) (a) * 0.9 0.9...

A fractionation column operating at 101 kPa is to separate 30 kgh of a solution of benzene and toluene containing 0.6 mass-fraction toluene into an overhead product containing 0.97 mass-fraction...

An auditor contacts an accounts receivable of the client directly in order to confirm the balance owing.This is an example of:Question 1 Select one:A . test of details of balances.B . tests of...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

Why is the System Build Process an iterative process?

What phase normally comes directly after the System Build process in a Project?

Name two other algorithms available in SSAS Data Mining other than Decision Trees.