Linear/Integer Programming

You are now responsible for placing orders and managing inventory for your company. The forecasting team has provided you with the following demand estimate over the next nine months:

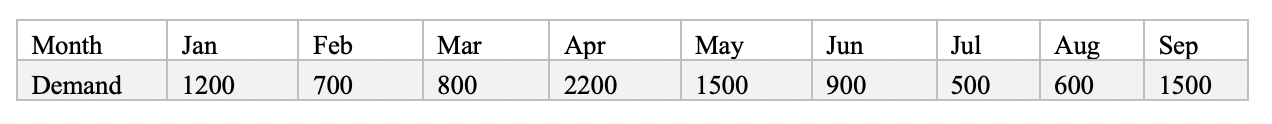There is a fixed setup cost (e.g., shipping and handling cost) of $3000 every time when you place an order from the supplier and the purchase cost is $1.00 per unit ordered. Orders are delivered by the supplier immediately. However, the supplier has limited production capacity and can provide at most 1800 units per order. We assume that the company can place at most one order at the beginning of each month (note: it is fine if you decide not to place an order in a month).

In addition to purchasing from the supplier, the company can also lease a 3D-printer and produce the toy model cars. There is a fixed leasing cost of $700 each month when you decide to lease the 3D-printer (note: you can choose not to lease the 3D-printer in a month), and the production cost is $1.50 per unit by using the 3D-printer. Your company can produce at most 500 units per month using this 3D-printer.

Your company does not allow unmet demand in each month. At the beginning of January, the company has only 200 units of product in its warehouse. Inventory cost of excess units is $0.50 per unit per month and the inventory costs are counted at the end of each month. At the end of September there should be at least 500 units in warehouse.

Develop a linear/integer programming spreadsheet model on Excel (with binary decision variables if needed) to determine the optimal timing and quantity of orders, whether and when to lease the 3D-printer, and the quantity of production using the 3D-printer, with the objective of minimizing the total cost.

Requirements of Solver and spreadsheet model format (follow the instructions below to avoid losing credits):

1. Be sure the integer optimality option (Solver Option) is set at 0%.

2. Color code the following components of the LP/IP model: given parameters, decisions, and the objective

3. Do NOT enter given parameters directly into equations or Solver.

\begin{tabular}{|l|l|l|l|l|l|l|l|l|l|} \hline Month & Jan & Feb & Mar & Apr & May & Jun & Jul & Aug & Sep \\ \hline Demand & 1200 & 700 & 800 & 2200 & 1500 & 900 & 500 & 600 & 1500 \\ \hline \end{tabular}