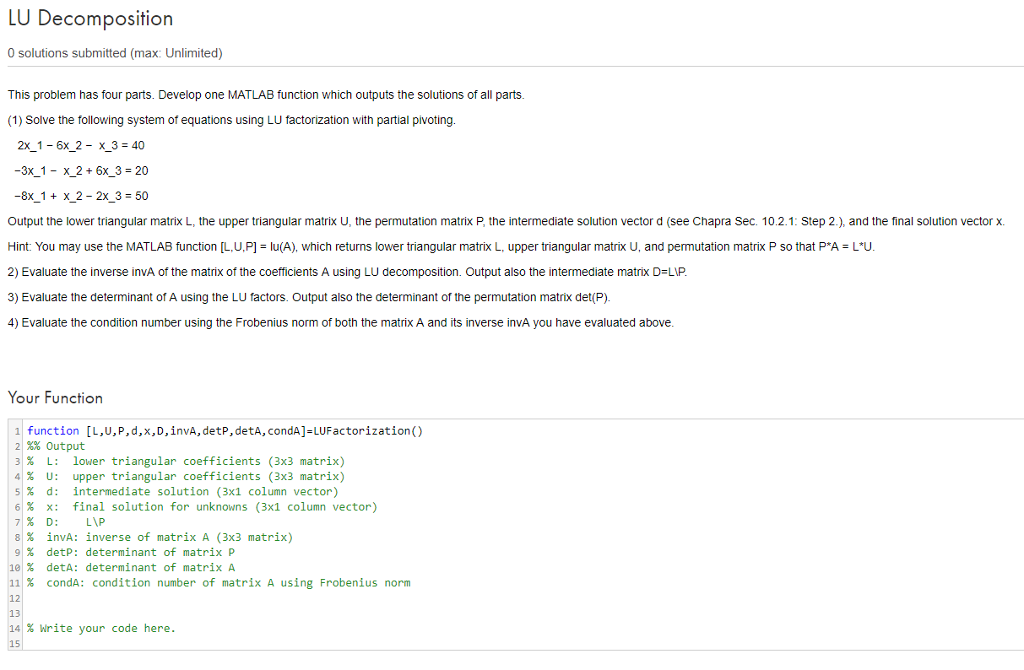
LU Decomposition 0 solutions submitted (max: Unlimited) This problem has four parts. Develop one MATLAB function which outputs the solutions of all parts. (1) Solve the following system of equations using LU factorization with partial pivoting 2x 1-6x 2- x 3 40 -3x 1- x 2 6x 3 - 20 -8x1 + x2-2x3 = 50 Output the lower triangular matrix L, the upper triangular matrix U, the permutation matrix P, the intermediate solution vector d (see Chapra Sec. 10.2.1: Step 2.), and the final solution vectorx. Hint You may use he MATLAB function LuP = u A , which returns lower nangular matrix L upper nangular mat xuan mutation matrix s a p A 2) Evaluate the inverse invA of the matrix of the coefficients A using LU decomposition. Output also the intermediate matrix D-LIP. 3) Evaluate the determinant of A using the LU factors. Output also the determinant or the permutation matrix detP 4) Evaluate the condition number using the Frobenius norm of both the matrix A and its inverse invA you have evaluated above. - - Your Function 1 function [L,U,P,d,x,D,invA, detP,detA, condAHUFactorization() 21%% Output 3 % L: lower triangular coefficients (3x3 matrix) 4 % U: upper triangular coefficients (3x3 matrix) 51% d: intermediate solution (3x1 column vector) 61% x: final solution for unknowns (3x1 column vector) 8 % invA: inverse of matrix A (3x3 matrix) 91% detp: determinant of matrix 1e% detA: determinant of matrix A % condA: condition number of matrix A using Frobenius norm % krite your code here