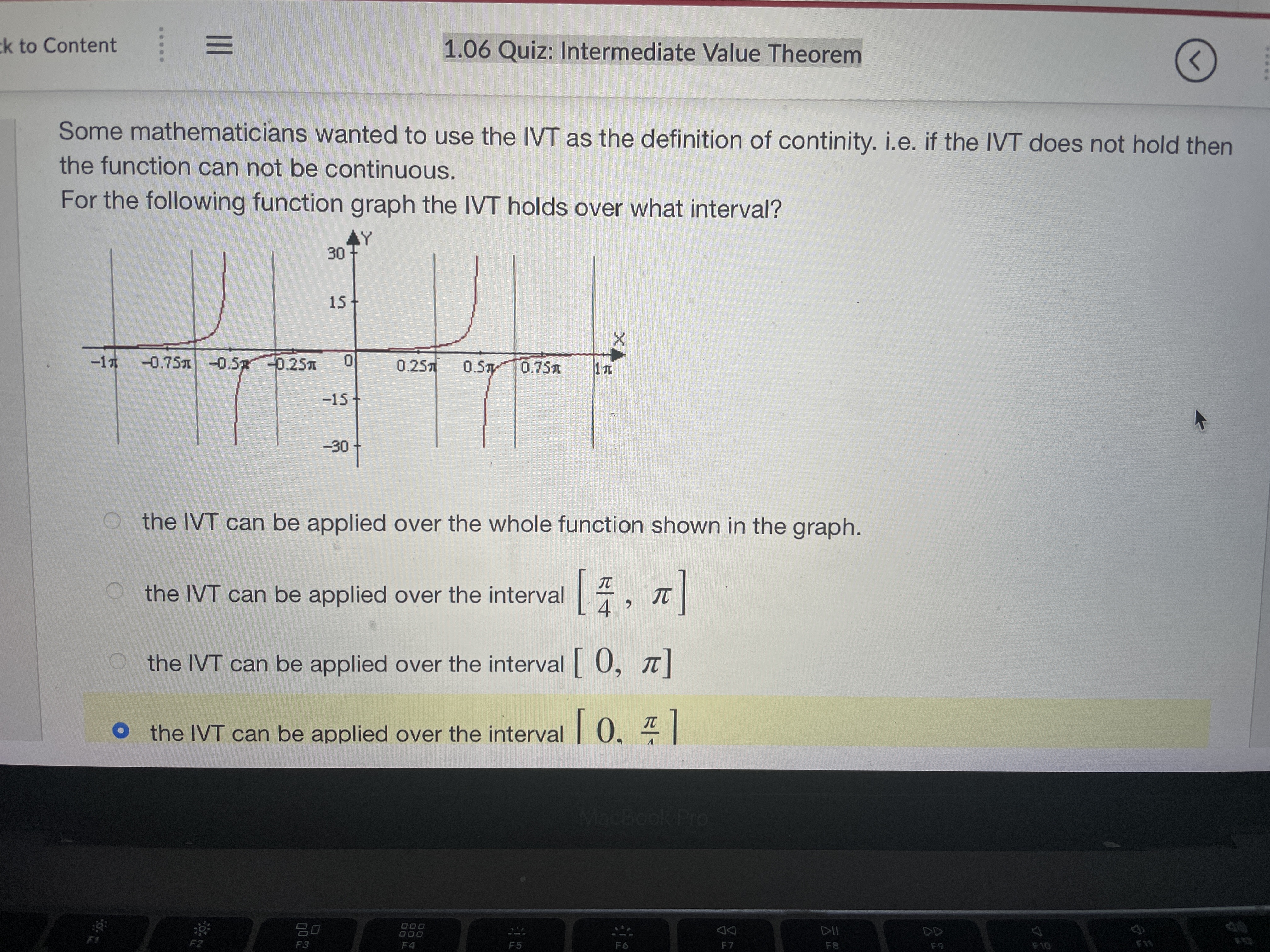
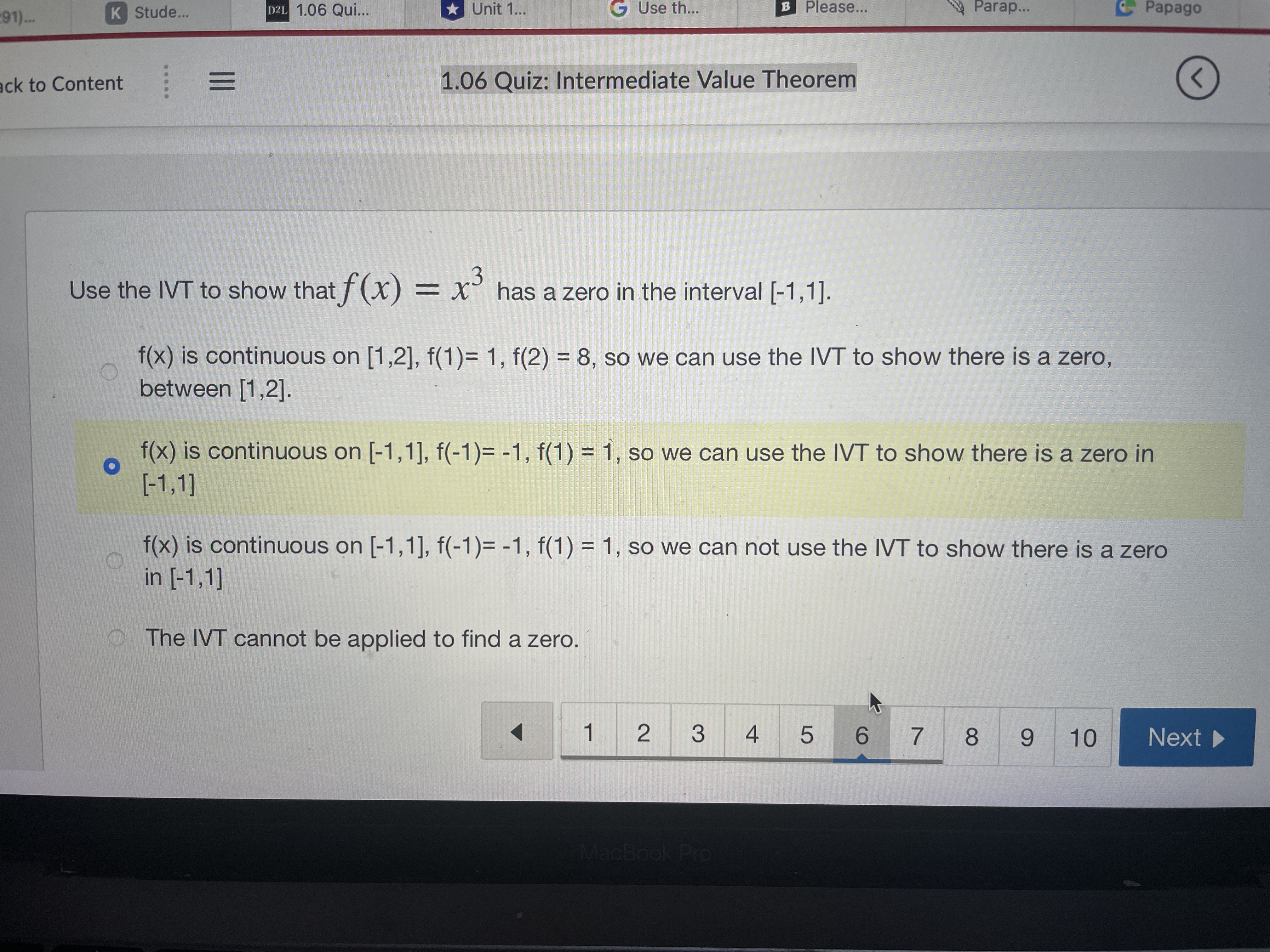
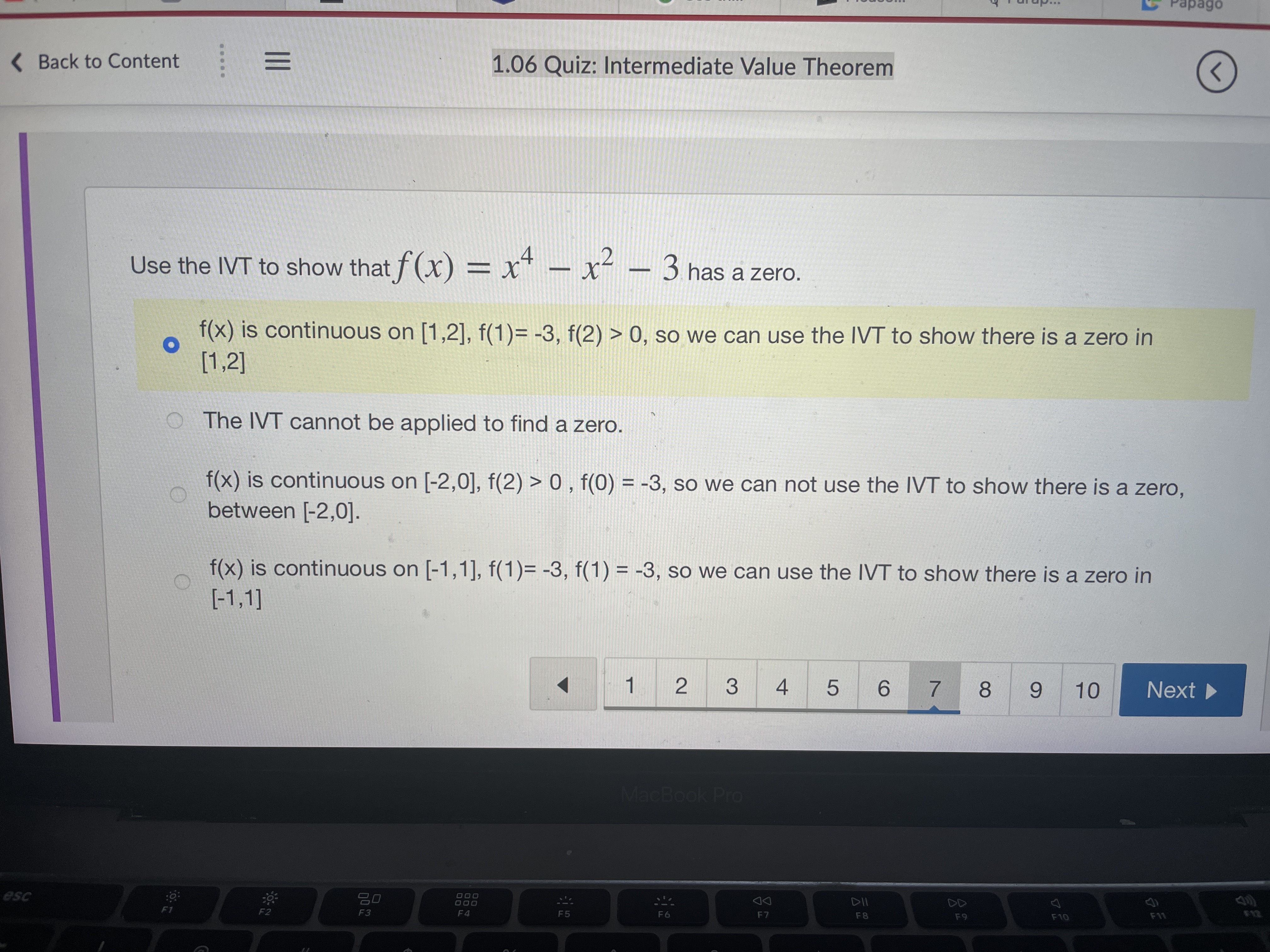
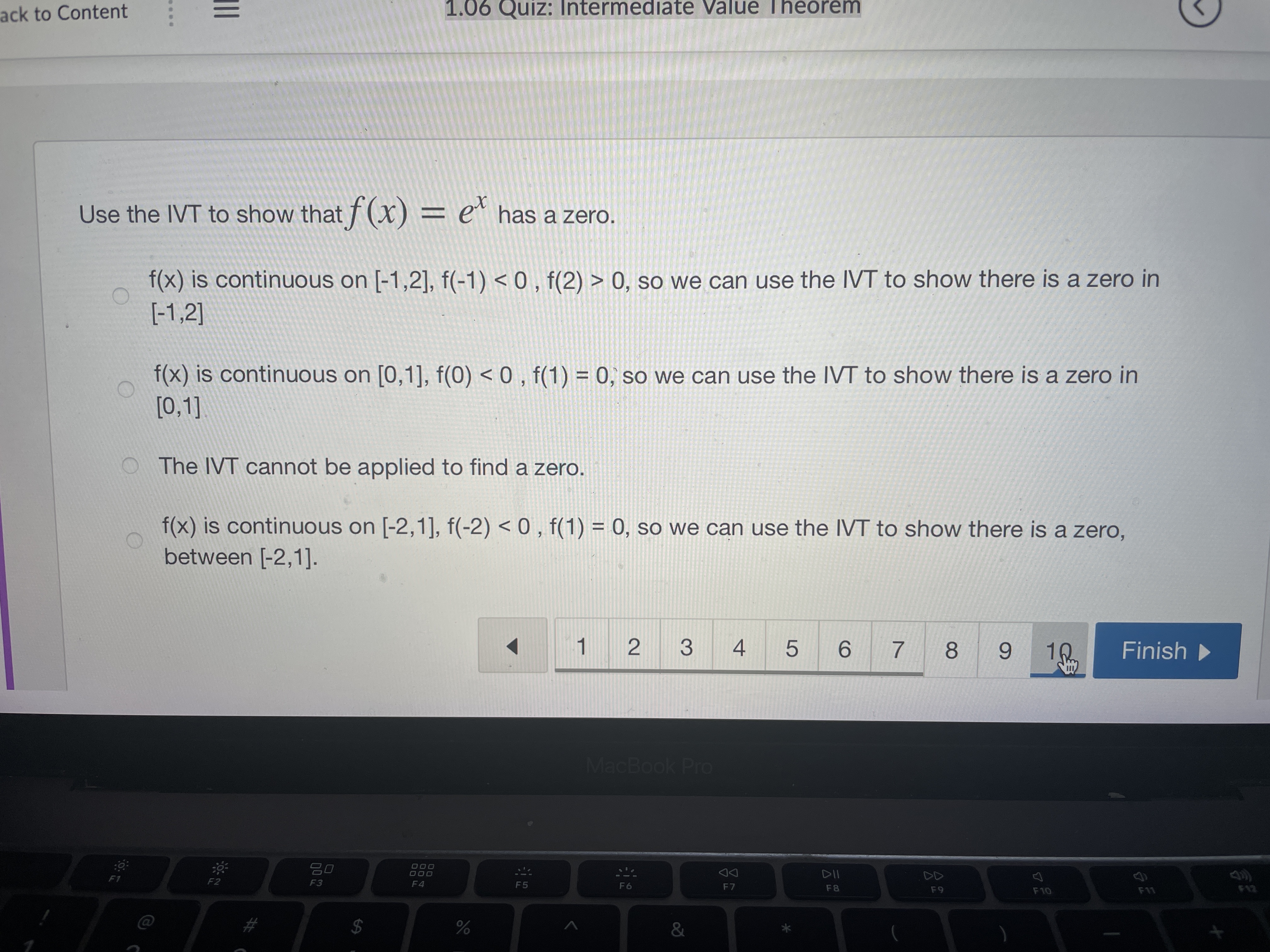
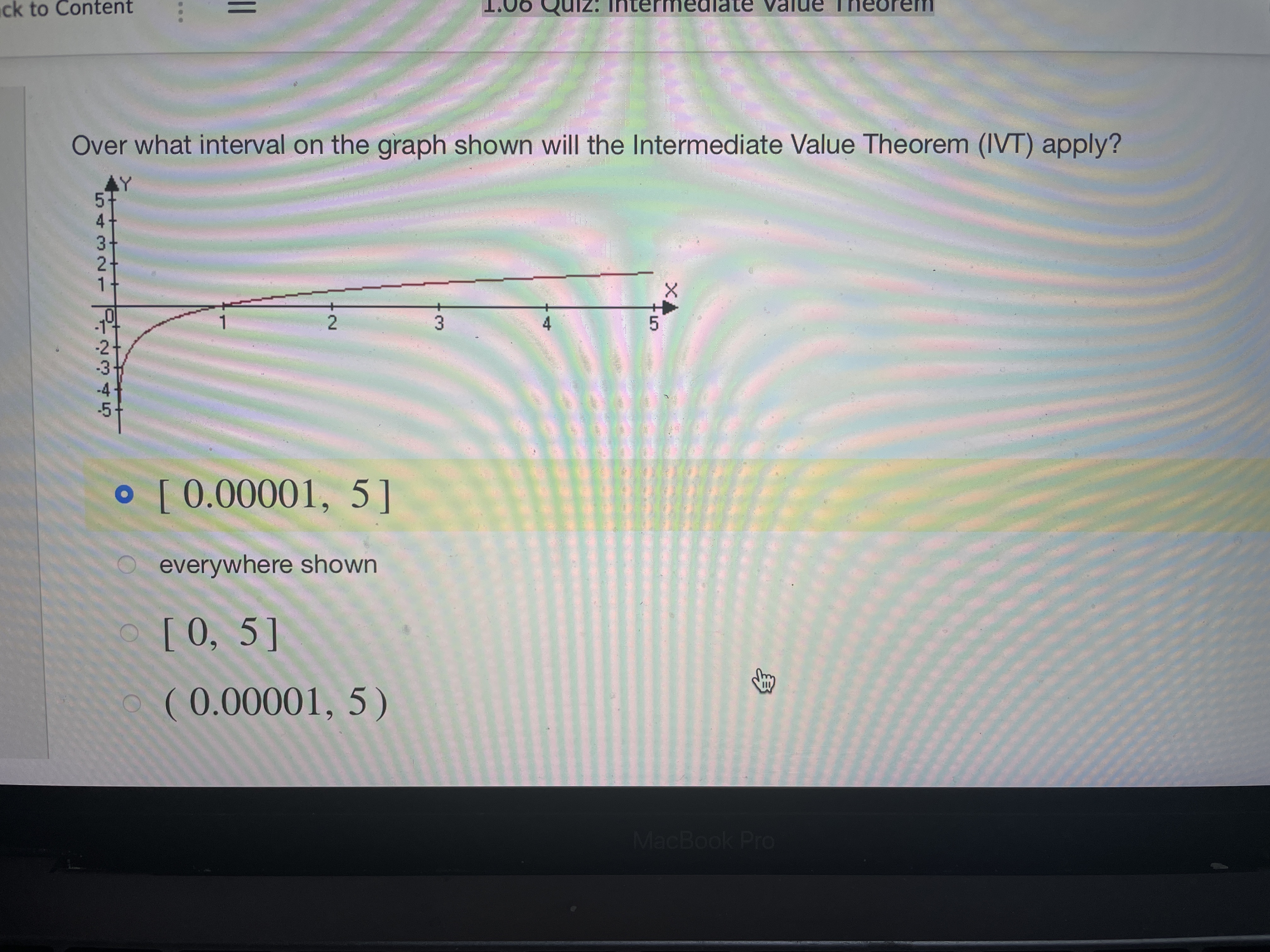
Question: m. ' Stude... w 'I.UD UUI... u UnlI'l... C Use In... .3 Please... W Parap... ' Paplgu ' i , u ck to Content
![NT to show there is a zero in [1.2] The lVT cannot](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666570111bbd5_85666657010ddccb.jpg)
![be applied to find a zero. f(x) is continuous on [-2,0], f(2)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66657011b3013_8576665701164d8d.jpg)
![NT to show there is a zero, between [-2,0]. f(x) is continuous](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66657012c98c3_858666570127c326.jpg)
![on [-1,1], f(1)= 3, f(1) = 3, so we can use the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666570136b33b_859666570131eae2.jpg)
![zero in [-1,2] You can use the IVT to show that there](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66657015cc486_861666570157bb8b.jpg)
![is a zero in [-1, 0] The IVT cannot be applied to](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666570164db49_8626665701610ae4.jpg)
![is a zero in [-1,1] 1 2 3 4 5 6 7Use](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66657017acb51_863666570172d5c5.jpg)
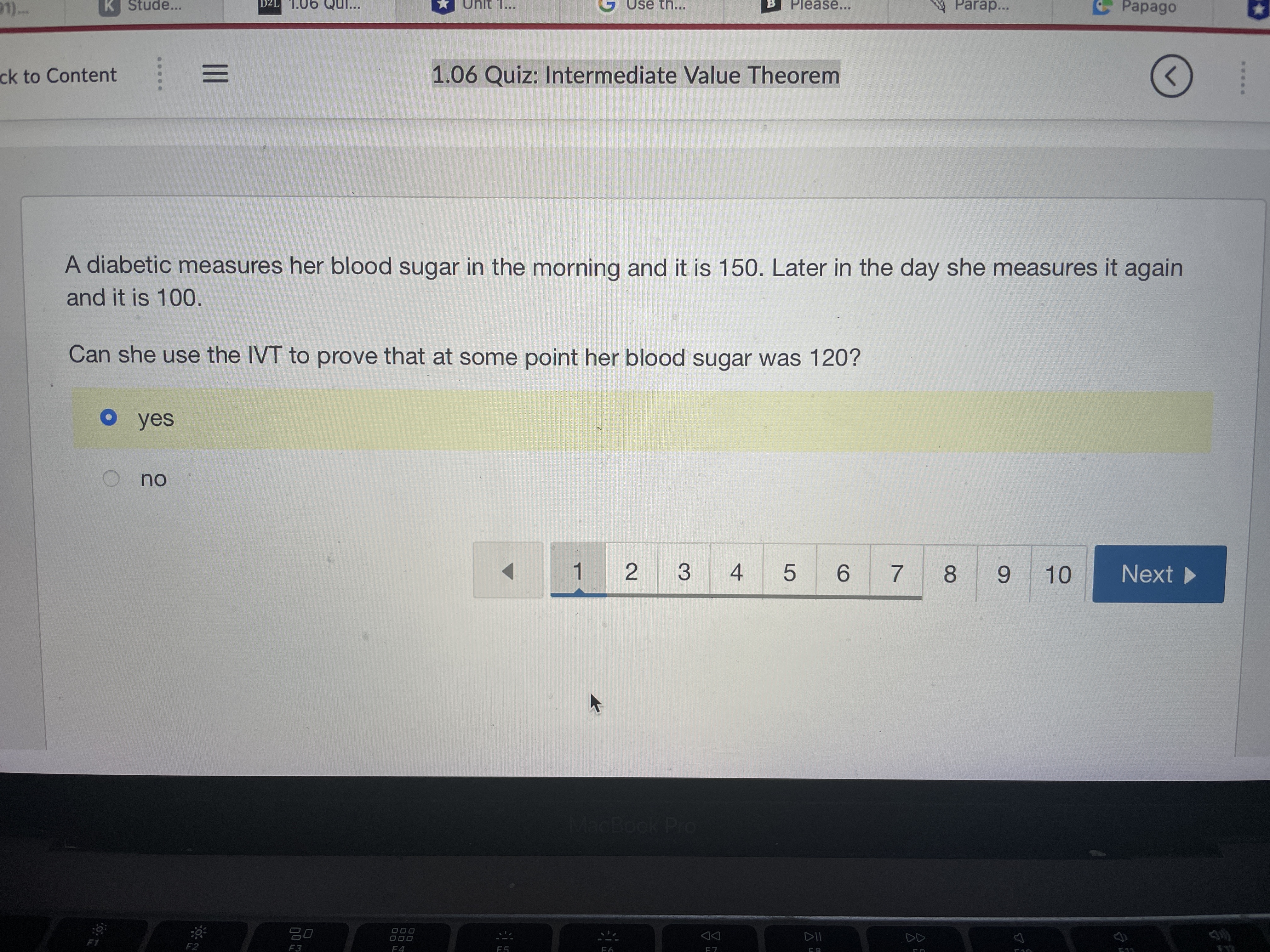
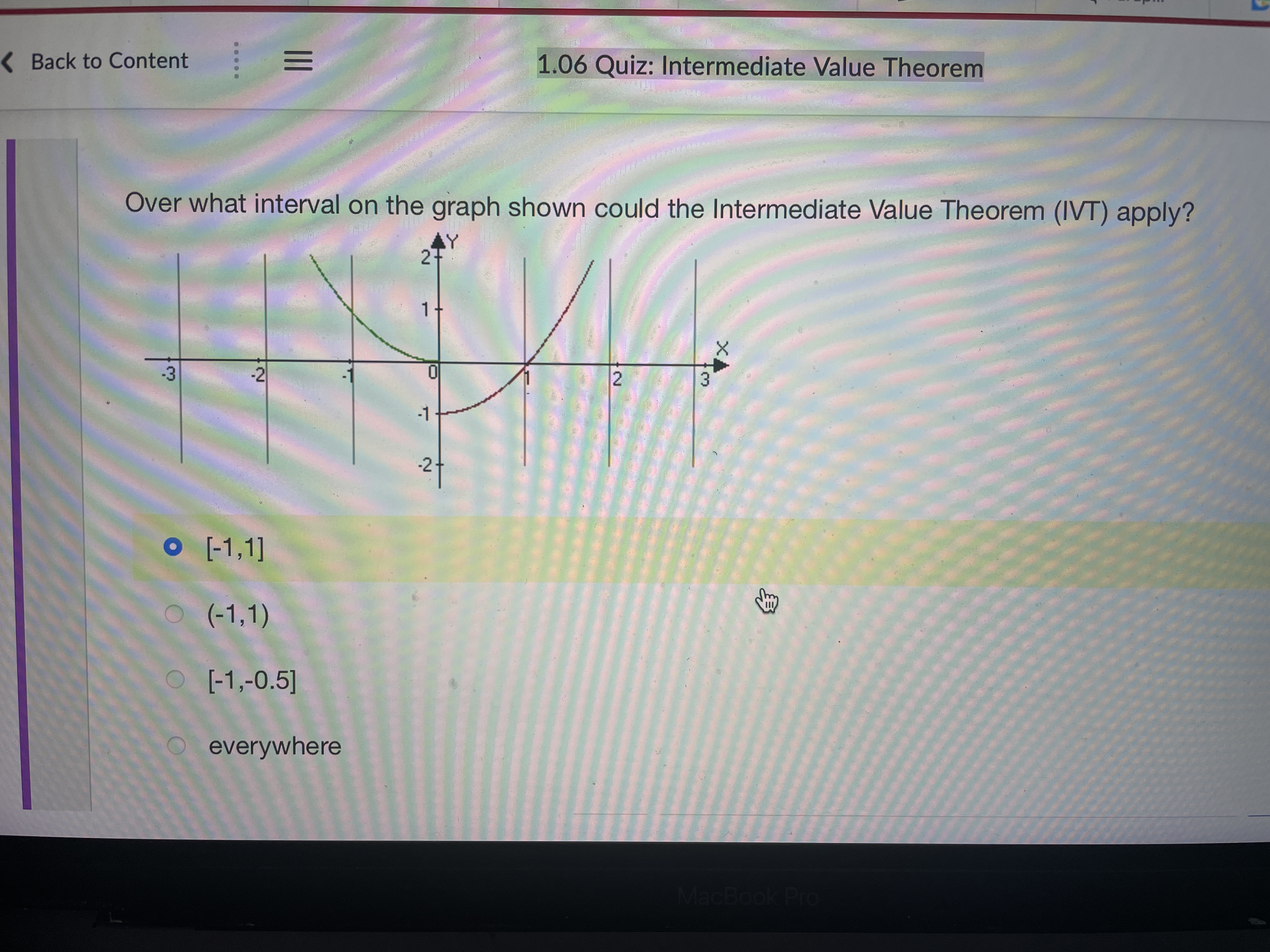
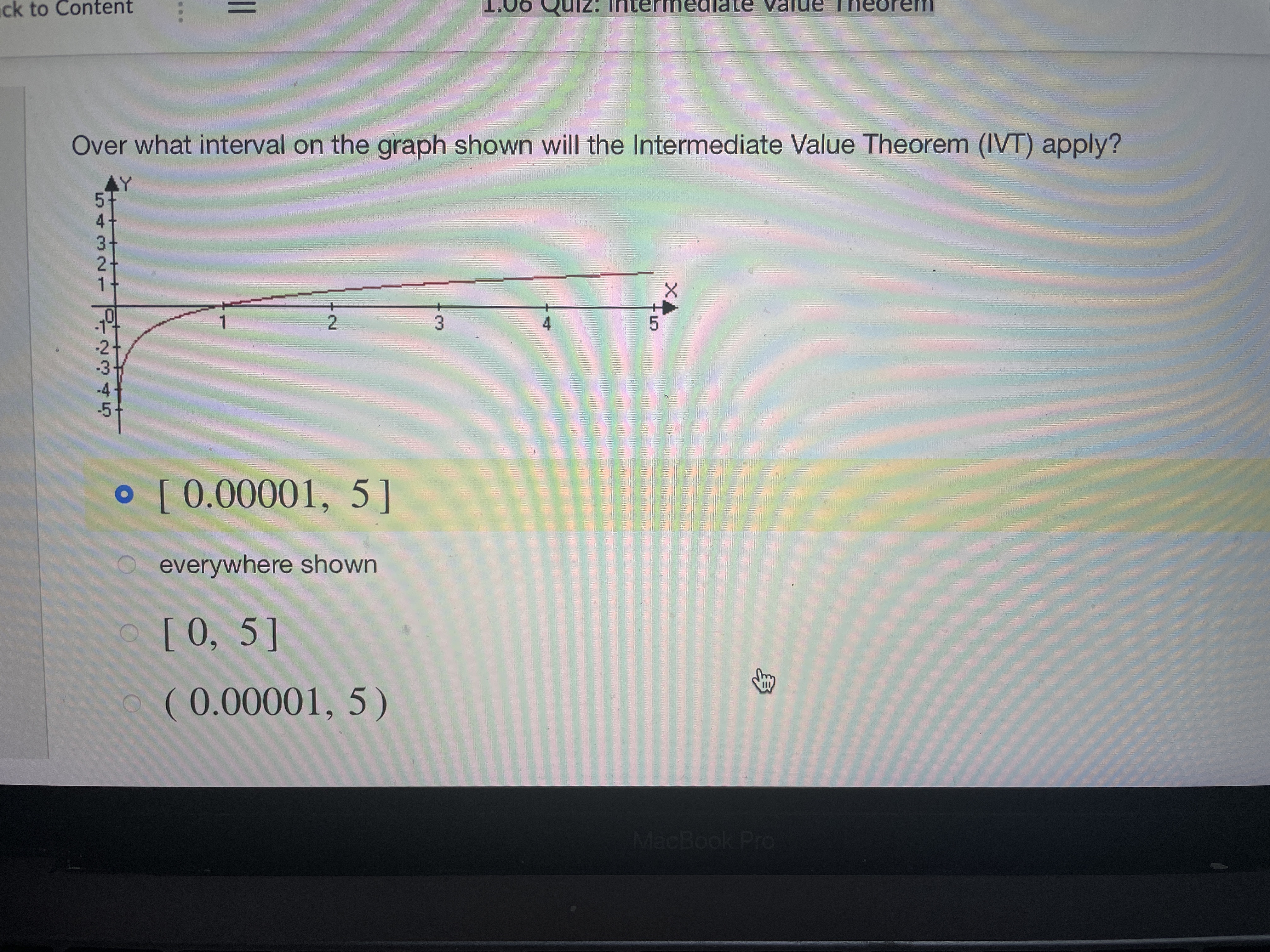
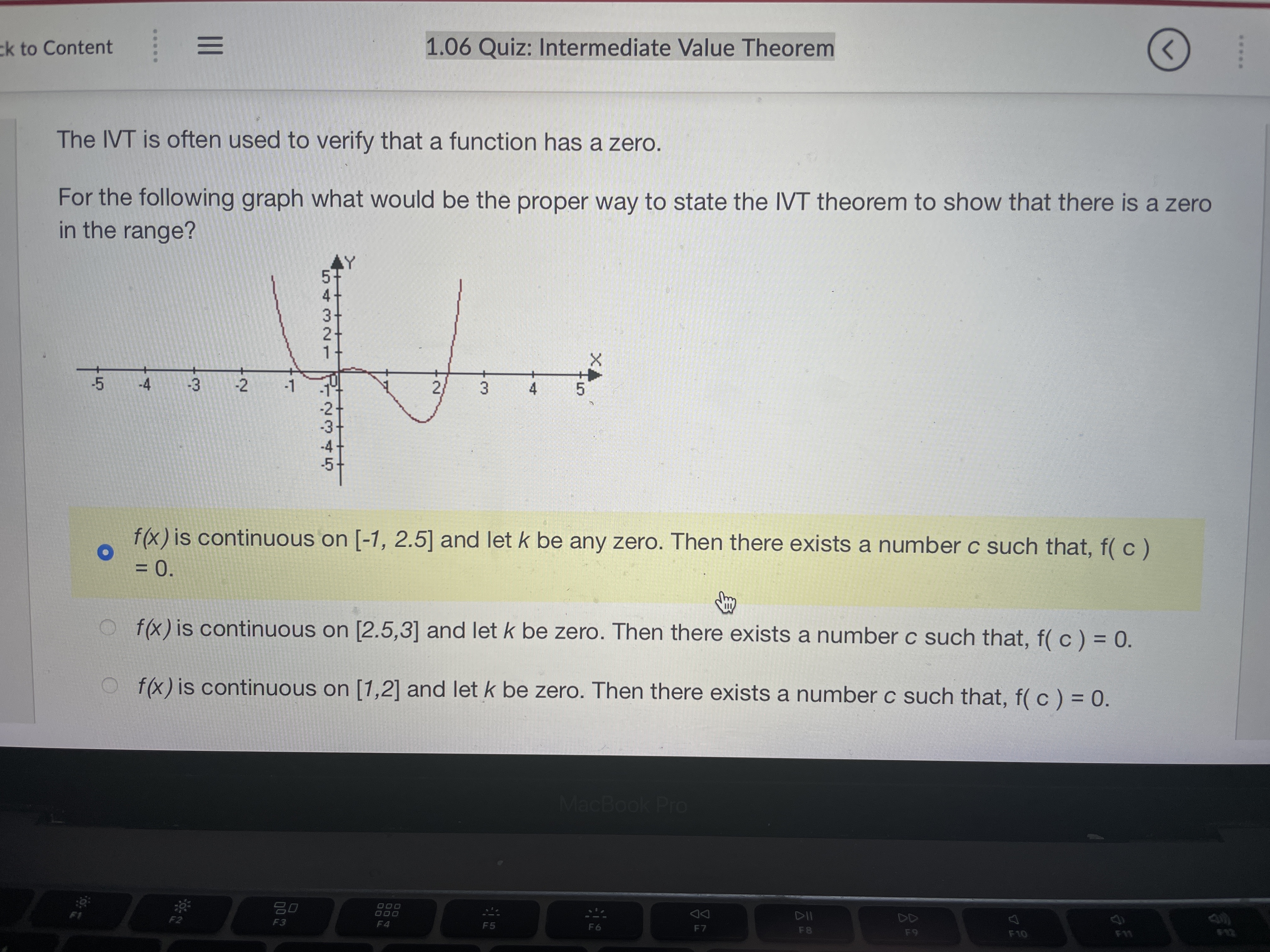
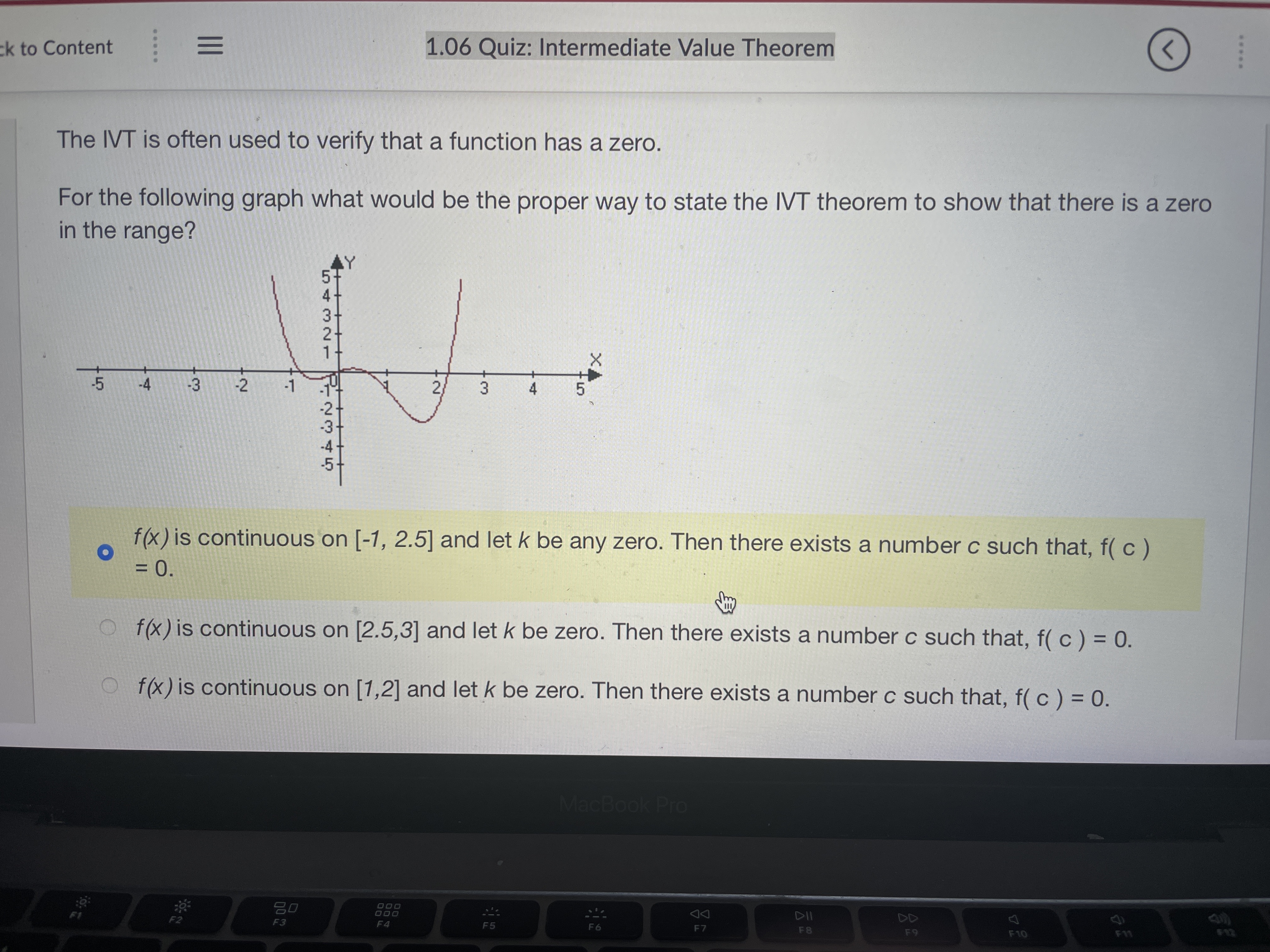
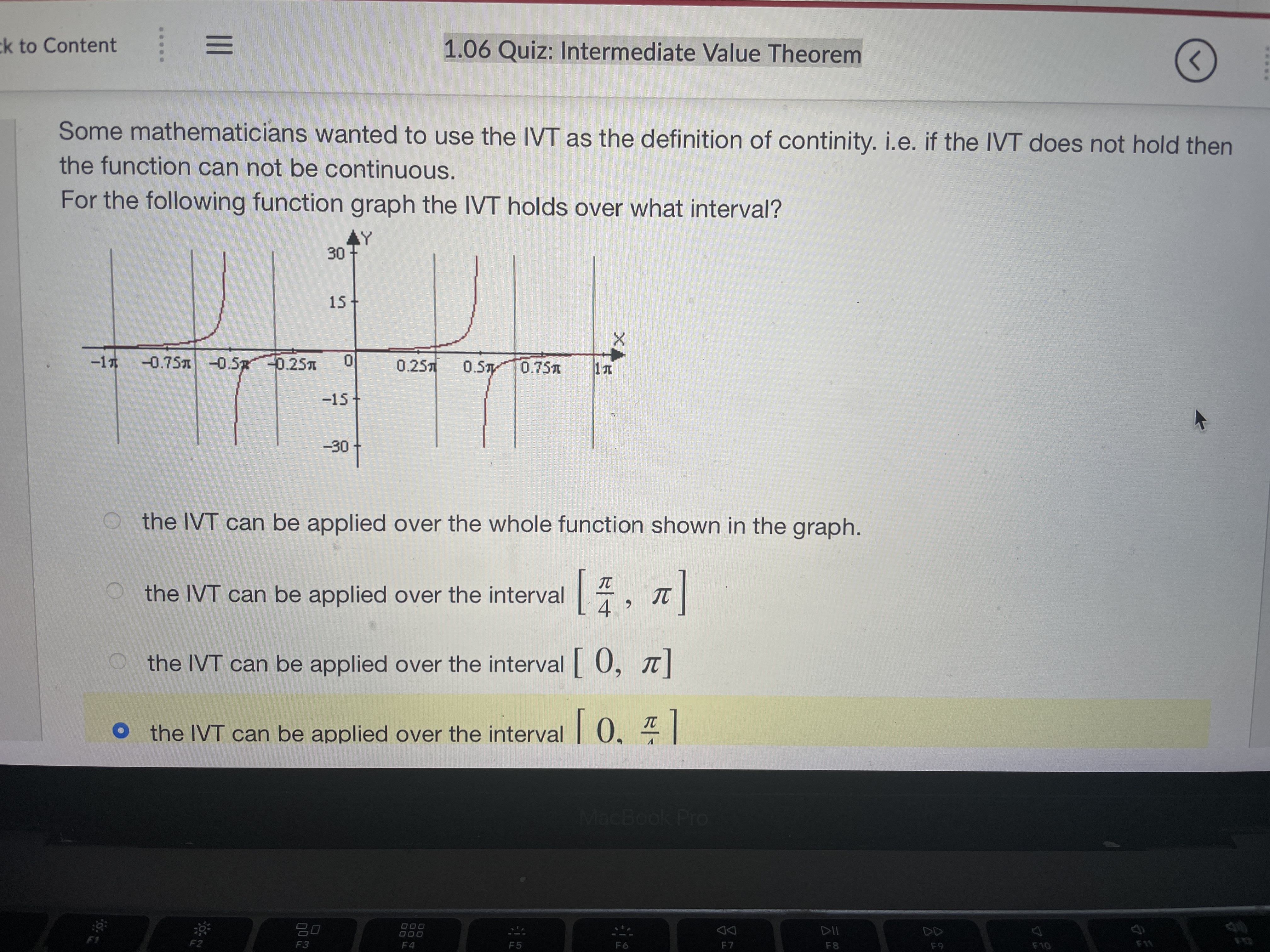
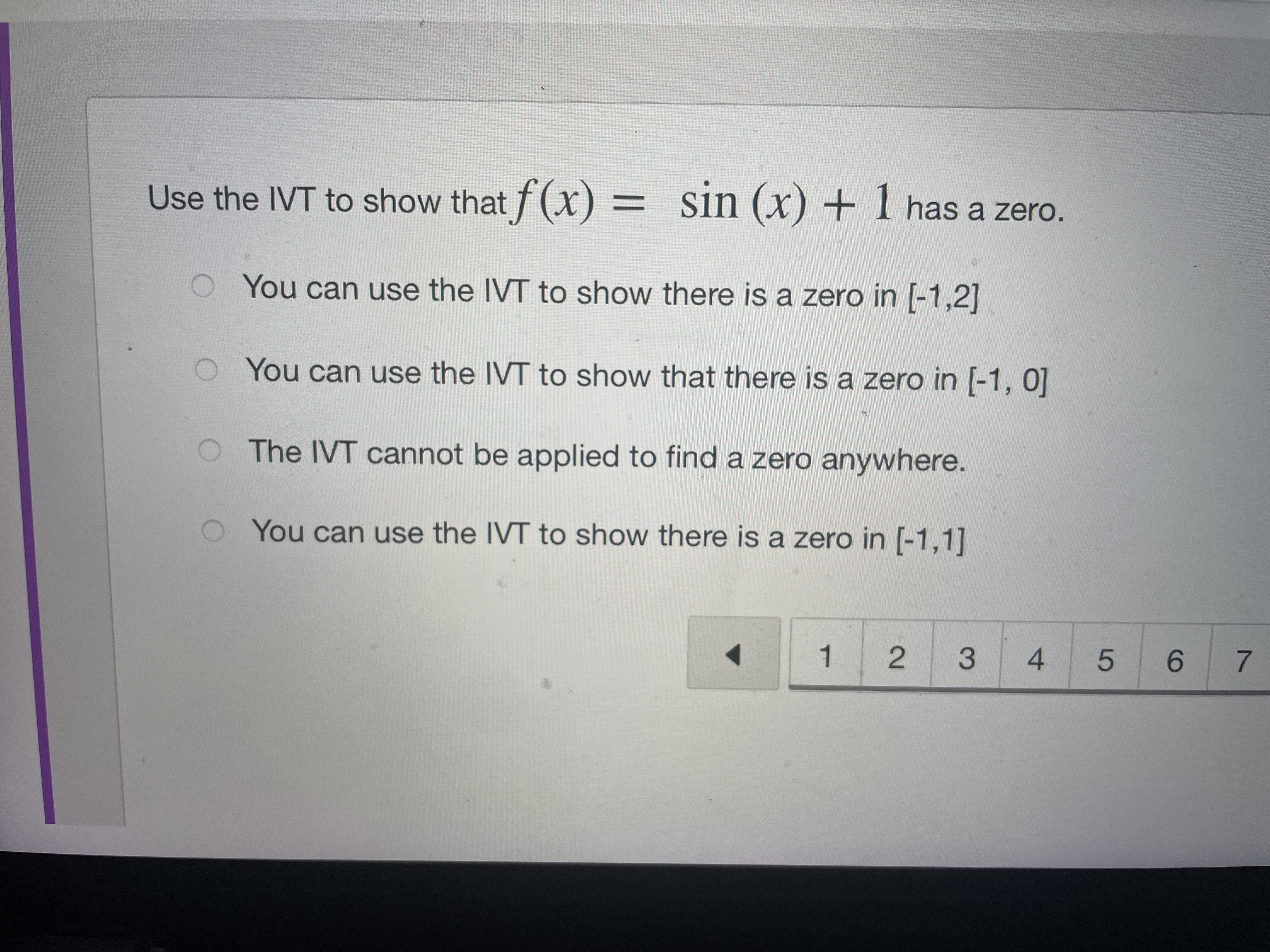
m. ' \" Stude... w 'I.UD UUI... u UnlI'l... C Use In... .3 Please... W Parap... ' Paplgu ' i , u ck to Content 1.06 Quiz: Intermediate Value Theorem 6) A diabetic measures her blood sugar in the morning and it is 150. Later in the day she measures it again and it is 100. Can she use the WT to prove that at some point her blood sugar was 120? 0 yes no 412345678910- we...\" 0, so we can use the NT to show there is a zero in [1.2] The lVT cannot be applied to find a zero. f(x) is continuous on [-2,0], f(2) > 0 , f(0) = -3, so we can not use the NT to show there is a zero, between [-2,0]. f(x) is continuous on [-1,1], f(1)= 3, f(1) = 3, so we can use the NT to show there is a zero in {-1.11 M Use the IVT to show that f (x) = sin (x) + 1 has a zero. You can use the IVT to show there is a zero in [-1,2] You can use the IVT to show that there is a zero in [-1, 0] The IVT cannot be applied to find a zero anywhere. You can use the IVT to show there is a zero in [-1,1] 1 2 3 4 5 6 7Use the IVT to show that f (x) = (x # 2) + 1 has a zero. O f(x) is continuous on [0, 1], f(0) 0, so we can use the IVT to show there is a zero in ['1 '2] f(x) is continuous on [0,1], f(O)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


