Make some quantitative assessments based upon knowledge of Markov chains for the board game Monopoly. In this question we are only concerned with the movement of a single player, as the movement of all players in the game is independent.

a) Develop a state transition matrix for Monopoly. It will be done in stages, or passes. In the first stage you will consider movement around the board due only to the dice. Develop the state matrix for dice only; disregard any instructions on the states in which you land. Generate a MATLAB (stem) graph of the invariant distribution. Make sure the horizontal axis goes from 0 to 39, and title the picture that reflects the fact that is dice only. Explain how you dervied this answer. What is 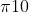? Does this make sense? Is this Markov chain periodic?

b) State 30, "Go to Jail", poses a modeling problem. If the dice tells us to go to e30, we immediately jump to e10 to complete our turn (trial). Thus, we never end up at e30, and 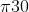=0. But "Go to Jail" plays an important role in the game. While the game Monopoly starts at e0, the Markov chain model can start with any initial probability distribution. What happens if we start at state e30 with probability one? Incorporate "Go To Jail" into the 2nd version of the state transition matrix. Develop a MATLAB stem plot of the invariant distribution (with state e30). Explain how you derived this answer. What is 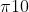? Does this make sense?

c) Develop the state transition matrix to incorporate "Chance". Develop a MATLAB stem plot of the invariant distribution. Label the graph with a title and number the states from 0 to 39. Explan how you derived this answer.

d) Develop the state transition matrix to incorporate "Community Chest". Develop a MATLAB stem plot of the invariant distribution. Explain how you derived this answer. What is the final ?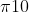

e) Starting at "Go" in the full game including Chance, Community Chest and "Go to Jail", what is the probability of getting to Park Place before going to Jail?

f) What color property group wiill give you the maximum expected rental income in the steady state? What is this expected income?

g) In the full model (dice, "Go To Jail", Chance and Community Chest), what is the probability of going to Jail in the steady-state by way of the Community Chest card?