Mantel produces a toy carriage, whose final assembly must include four wheels and two

seats. The factory producing the parts operates three shifts a day. The following table

provides the amounts produced of each part in the three shifts:

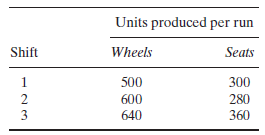
Ideally, the number of wheels produced is exactly twice that of the number of seats. However, because production rates vary from shift to shift, exact balance in production may not be possible. Mantel is interested in determining the number of production runs in each shift that minimizes the imbalance in the production of the parts. The capacity limitations restrict the number of runs to between 4 and 5 for shift 1, 10 and 20 for shift 2, and 3 and 5 for shift 3. Formulate the problem as a GP model.

\begin{tabular}{ccc} \hline & \multicolumn{2}{c}{ Units produced per run } \\ \cline { 2 - 3 } Shift & Wheels & Seats \\ \hline 1 & 500 & 300 \\ 2 & 600 & 280 \\ 3 & 640 & 360 \\ \hline \end{tabular} \begin{tabular}{ccc} \hline & \multicolumn{2}{c}{ Units produced per run } \\ \cline { 2 - 3 } Shift & Wheels & Seats \\ \hline 1 & 500 & 300 \\ 2 & 600 & 280 \\ 3 & 640 & 360 \\ \hline \end{tabular}