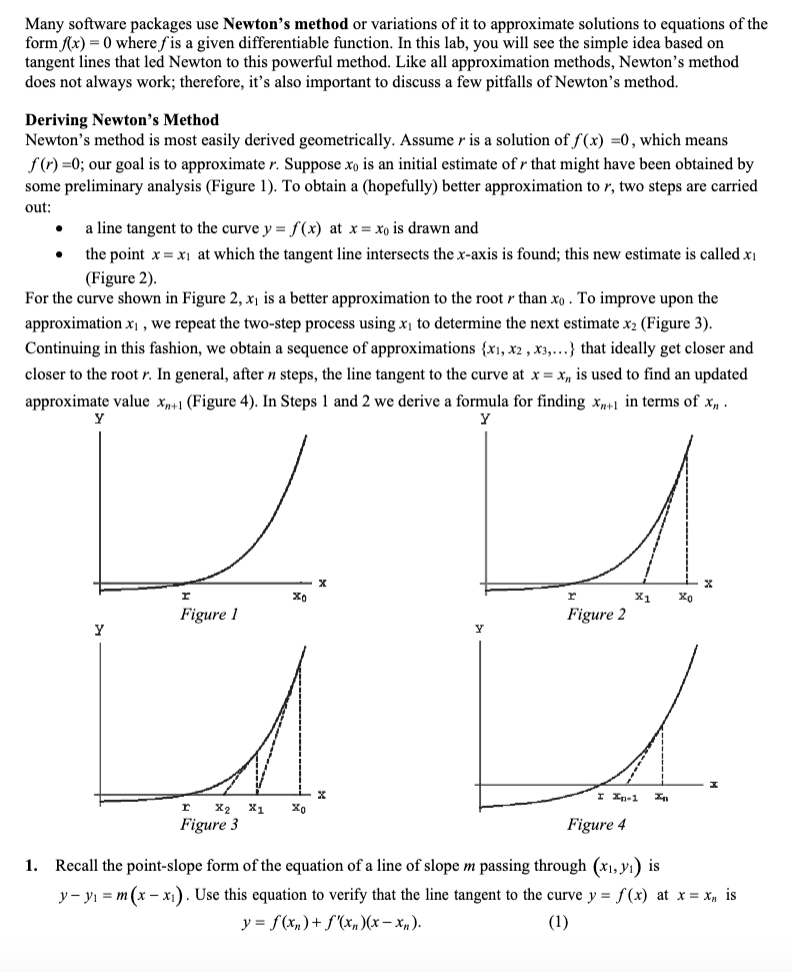
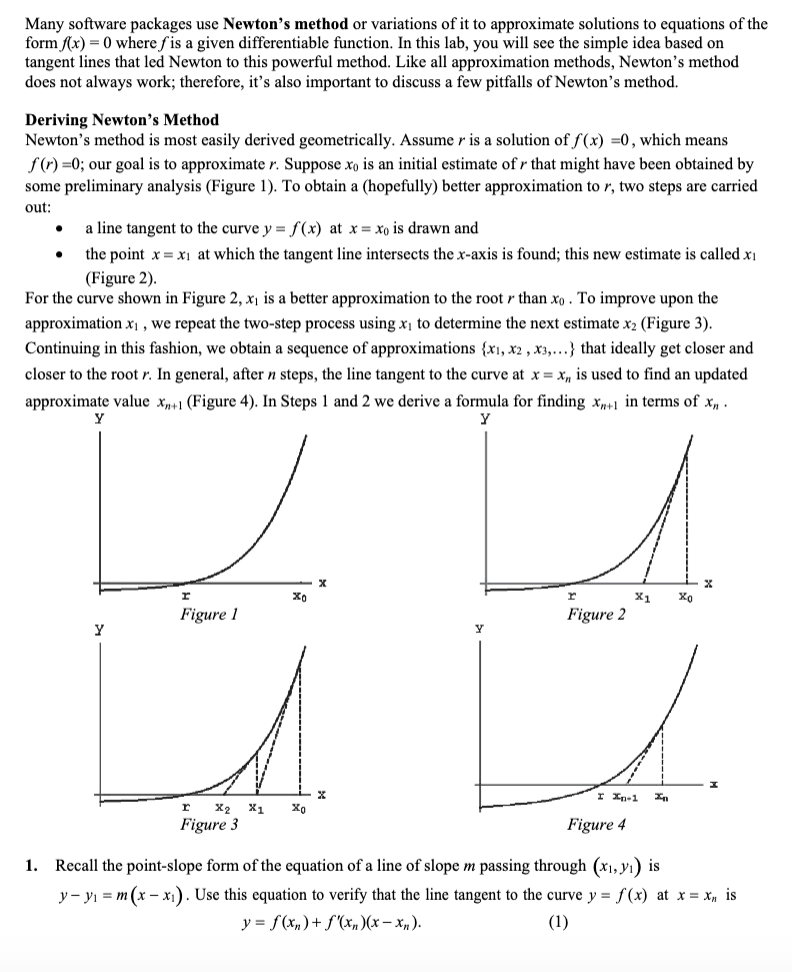
Many software packages use Newton's method or variations of it to approximate solutions to equations of the formx) = 0 where f is a given differentiable inetionl In this lab. you will see the simple idea based on tangent lines that led Newton to this powerful method. Like all approximation methods. Newton's method does not always work; therefore, it's also important to discuss a few pitfalls of Newton's method. Deriving Newton's Method Newton's method is most easily derived geometrically. Assume r is a solution of If (x) =0 , which means f(r} :0; our goal is to approximate r. Suppose xu is an initial estimate of r that might have been obtained by some preliminary analysis ( Figure 1). To obtain a (hopefully) better approximation to r. two steps are carried {Juli a a line tangent to the curve y = If\") at x = x0 is drawn and o the point x = M at which the tangent line intersects the x-ax is is found; this new estimate is called in (Figure 2}. For the curve shown in Figure 2, XI is a better approximation to the root r than xu . To improve upon the approximation x1 , we repeat the twostep process using in to determine the next estimate x; (Figure 3). Continuing in this fashion. we obtain a sequence of approximations {xn x2 , X3.n.} that ideally get closer and closer to the root r. In general. utter :1 steps. the line tangent to the curve at x = x" is used to find an updated approximate value xml (Figure 4) [n Steps l and 2 we derive a formula for nding .rml in terms of x,, _ Y Y I x; Kg Figure 2 gure 3 Figure 4 1. Recall the point-slope form of the equation of a line of slope in passing through (x1, y1) is yy1 = m(x x.) . Use this equation to verify that the line tangent to the curve y = f(x) at x = x\" is y=ftxnl+f'(xn}(X-xn)- (1) 2. Assume the tangent line represented by equation (1) intersects the x-axis at x = X, ] and verify that updated approximation approximation approximation f (x ] n+1 (2) (x m ) approximation Using equation (2) with n = 0, 1, 2, 3, ..., the current approximation x,, is used to obtain a (hopefully) improved approximation X,+1 . The resulting sequence of approximations {xo, X1, x2, ...} often approaches a root of f very quickly