Markov Analysis

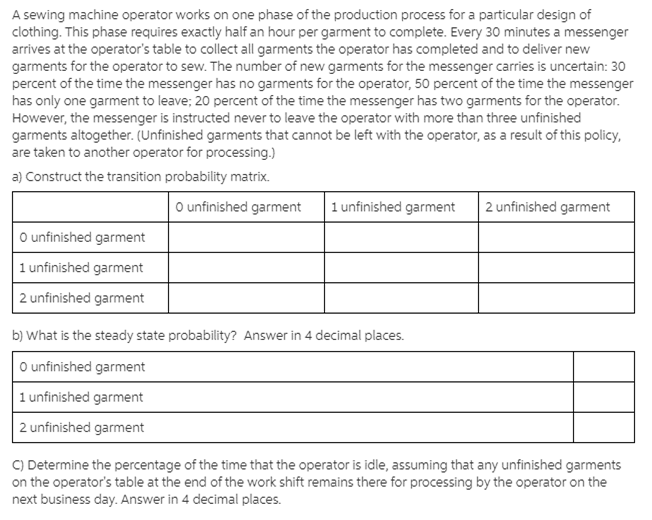
A sewing machine operator works on one phase of the production process for a particular design of clothing. This phase requires exactly half an hour per garment to complete. Every 30 minutes a messenger arrives at the operator's table to collect all garments the operator has completed and to deliver new garments for the operator to sew. The number of new garments for the messenger carries is uncertain: 30 percent of the time the messenger has no garments for the operator, 50 percent of the time the messenger has only one garment to leave; 20 percent of the time the messenger has two garments for the operator. However, the messenger is instructed never to leave the operator with more than three unfinished garments altogether. (Unfinished garments that cannot be left with the operator, as a result of this policy, are taken to another operator for processing.) a) Construct the transition probability matrix. O unfinished garment 1 unfinished garment 2 unfinished garment O unfinished garment 1 unfinished garment 2 unfinished garment b) What is the steady state probability? Answer in 4 decimal places. O unfinished garment 1 unfinished garment 2 unfinished garment C) Determine the percentage of the time that the operator is idle, assuming that any unfinished garments on the operator's table at the end of the work shift remains there for processing by the operator on the next business day. Answer in 4 decimal places. A sewing machine operator works on one phase of the production process for a particular design of clothing. This phase requires exactly half an hour per garment to complete. Every 30 minutes a messenger arrives at the operator's table to collect all garments the operator has completed and to deliver new garments for the operator to sew. The number of new garments for the messenger carries is uncertain: 30 percent of the time the messenger has no garments for the operator, 50 percent of the time the messenger has only one garment to leave; 20 percent of the time the messenger has two garments for the operator. However, the messenger is instructed never to leave the operator with more than three unfinished garments altogether. (Unfinished garments that cannot be left with the operator, as a result of this policy, are taken to another operator for processing.) a) Construct the transition probability matrix. O unfinished garment 1 unfinished garment 2 unfinished garment O unfinished garment 1 unfinished garment 2 unfinished garment b) What is the steady state probability? Answer in 4 decimal places. O unfinished garment 1 unfinished garment 2 unfinished garment C) Determine the percentage of the time that the operator is idle, assuming that any unfinished garments on the operator's table at the end of the work shift remains there for processing by the operator on the next business day. Answer in 4 decimal places