Markov chain

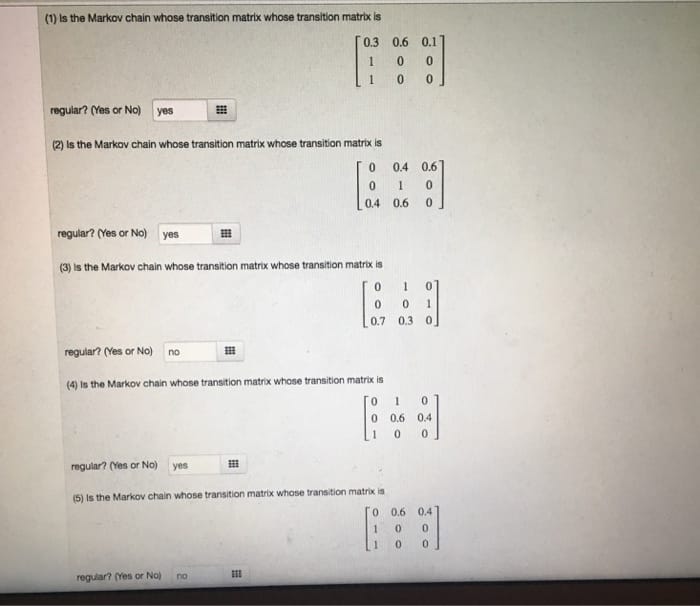
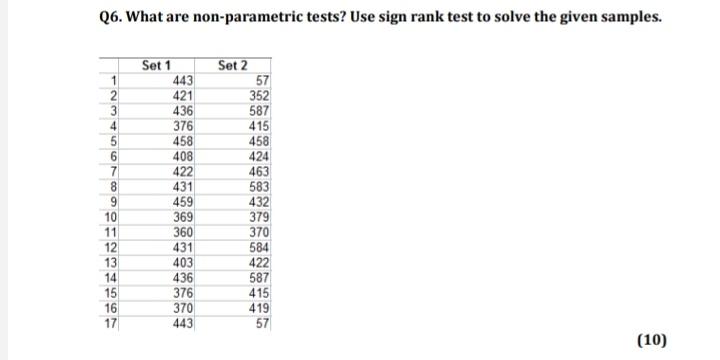
(1) Is the Markov chain whose transition matrix whose transition matrix is 0 regular? (Yes or No) yes (2) Is the Markov chain whose transition matrix whose transition matrix is 0 0.4 0.6 0 1 0 0.4 0.6 0 regular? (Yes or No) yes (3) is the Markov chain whose transition matrix whose transition matrix is regular? (Yes or No) no (4) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0 0.6 0.4 0 regular? (Yes or No) yes (5) Is the Markov chain whose transition matrix whose transition matrix is regular? (res or No) naConsider a Markov chain {Xn, n = 0, 1, . . .} on the state space S = {0, 1, 2}. Suppose that the Markov chain has the transition matrix 4 10 10 10 P = 4 3 10 10 10 2 4 10 10 10 1. Show that the Markov chain has a unique stationary mass. 2. Let h denote the stationary mass of the Markov chain. Find h(x) for all x E S. 3. Show that the Markov chain has the steady state mass. 4. Let h* denote the steady state mass of the Markov chain. Find h* (x) for all x E S.Q6. What are non-parametric tests? Use sign rank test to solve the given samples. Set 1 Set 2 443 57 421 352 436 587 376 415 458 458 408 424 422 463 431 583 459 432 369 379 11 360 370 12 431 584 13 403 422 14 436 587 15 376 415 16 370 419 17 443 57 (10)Q6. What are non-parametric tests? Use sign rank test to solve the given samples. Set 1 Set 2 443 57 421 352 436 587 376 415 458 458 408 424 422 463 431 583 459 432 369 379 11 360 370 12 431 584 13 403 422 14 436 587 15 376 415 16 370 419 17 443 57 (10)Consider a bivariate normal population with #1 = 0, /2 = 2, 011 = 2, 622 = 1, and P12 = 0.5. (a) Write out the bivariate normal density. (b) Write out the squared generalized distance expression (x - p)'E-1(x - ) as a function of x, and x2. (c) Determine and sketch the constant-density contour that contains 50% of the probability.Consider a bivariate normal population with #1 = 0, /2 = 2, 011 = 2, 622 = 1, and P12 = 0.5. (a) Write out the bivariate normal density. (b) Write out the squared generalized distance expression (x - p)'E-1(x - ) as a function of x, and x2. (c) Determine and sketch the constant-density contour that contains 50% of the probability