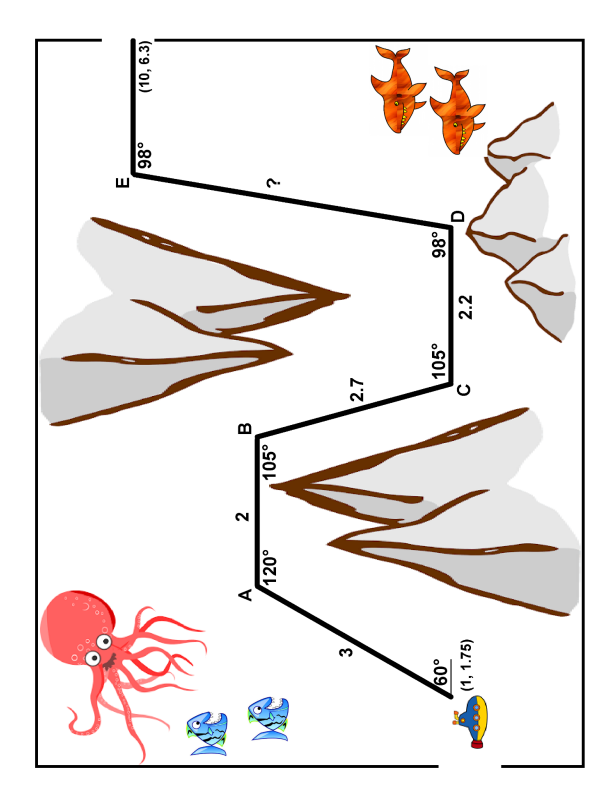
MATH 1111 : Chapter 6 : Lab 6.1 Name 1) For an acute angle 0, suppose tan (O) =. Compute exact and approximate values of cos(0). 2) For an acute angle 0, suppose cos(0) = > Compute exact and approximate values of tan(@). 3) A tree standing vertically on level ground casts a 35 foot long shadow. The angle of elevation from the end of the shadow to the top of the tree is 61.7. Determine the height of the tree.Approximate the following to 5 decimal places. 4) 5) 6) 7) 8) Approximate tan(73%) Approximate cos (%") Approximate cos(377) 2" Approximate cot (T) Approximate tan(26) 9) Calculate all angles and all sides of the right triangle with hypotenuse 83 and one angle 57. 7 10) For an acute angle 8, suppose tan(@) = 3 Approximate the measurement of the angle in degrees and radians. 11) Steven is standing in a field. He walks 20 yards due East and then 30 yards due North and then 15 yards due East and then 5 yards due North. a. How far did Steven walk? b. How far is Steven from his original standing position? 12} A submarine has entered the ocean scene on the next page. Its initial position is (1, 1.75). It follows the path indicated to the other side of the screen and exits through the opening at position (10, 6.3). (The drawing is not to scale.) The path is marked with angles and distances. The angles are in degrees and the distances are in miles. Calculate the coordinates for the following points: m What is the distance between the points D and E? The submarine travels at a speed of 0.7 miles per hour. How long does it take to go from entering to exiting the screen? \fDegrees A full rotation is 360 degrees Uses a symbol . for measurements. Example, 90 Commonly used in nearly all applications Can be expressed as decimals or broken into minutes and seconds of angle. 45.51' = 45"30'36" We will not use degrees/minutes/seconds in this class. The measurement system of degrees dates back to ancient Babylon. The Babylonians used a base 60 system, as opposed to our own base 10. You'll learn more about number bases in Chapter 10. The Babylonians are also where we get 60 seconds in a minute, 60 minutes in an hour. The choice of 60 was arbitrary, but useful. Sixty is a number that an be divided evenly by many prime numbers. Consider how many ways you can divide 360 By 2. Half a turn is 180 By 3. A third of a turn is 120 By 4. A quarter turn is 90 By 5. A fifth in 72" By 6. 60 By 8. 45" By 9. 40' By 10. 36 And more We can divide by every single digit number except seven and get an integer result. Consider a world where a full rotation was a base ten number like 100. We'd be able to divide by 2, 4, 5, 10, 20, 25, 50, and 100. That's it. Any other number would result in fractions, many of them ugly. This extreme divisibility is why degrees are still in use today.Conversions 160 Converting from radians to degrees is simple. Multiply the radians by - Done. Converting from degrees to radians is simple. Multiply the degrees by % Dane. Identifying the angle measurement. The ONLY thing that matters is the presense of the mark. Radians don't have a unit mark; the Greeks treated angle measurements as a ratio of lengths and were thus unitless. Modern physics agrees with that inter pretation. The following are examples of degrees The following are examples of radians