MATH 1324 Assessment

Linear Programming Project

1. Introduction

In many business and economic problems, we seek to optimize (maximize or minimize) a function -such as profit or cost- subject to certain constraints, such as limitations on resources.

Problems of this nature in which both the targeted function and the constraints are expressed as linear equations or inequalities are called linear programming problems.

In this project, you will solve a linear programming problem.

1. Instructions

This project consists of the following steps:

1. Choose a problem for your project from the section "List of Linear Programming Problems". ( Be sure your choice is approved by your instructor.)
2. Solve the problem you chose (with instructor's approval) in step 1 above.

• Type the problem statement together with the problem number as the title.
• Include a table with your subjective inequalities for the constraints and the objective function to be optimized. Assign variables.
• Include a graph of the feasible set using Desmos Graphing Calculator. Make sure the points coordinates are visible by double clicking each corner point of the feasible area.
• Take a screenshot and paste the graph into your presentation.
• Test each of the points with your objective function to determine the maximum or minimum of the problem.
• Get your solution in terms of the problem and elaborate on why this solution is important. You may have to do a little research.

1. Grading Rubric

Your grade on this project will be determined based on the accuracy, exposition, and thorough explanation of your work on each of the following items:

Components	Points	Checklist
Write the problem stated as a linear programming problem. (40%)	40 total
Generate the linear programming problem	5
Assign Variables	5
Describe the objective function	5
Generate the constraints as inequalities	15
Tabulate the information given in your problem	10
Solve the Linear Programming Problem (50%)	50 total
Graph the feasible set S	15
Find and list the coordinates of all corner points	10
Evaluate the objective function at each corner point	10
Describe the corner point that optimizes the objective function and write it in terms of the problem Elaborate on the answer	15
Aesthetics (10%)	10 Total
Include a cover and the original problem statement	5
Use appropriate sized font, a professional layout, and proper grammar	5
Total	100

Note: Kindly pick one of these problems below

Real Estate Development:

A real estate developer wants to maximize the profit from selling residential properties. The developer has limited resources and needs to decide how many units of different types of properties to build. The developer has the following constraints: Building a customized luxury house generates a profit of $425,000 per unit since it will use high end materials and wall treatments, while building a standard builder grade house generates a profit of $150,000 per unit. Building a luxury house requires 4 months of construction time, while building a standard house requires 2 months of construction time.The developer has a total of 4 years available for construction and can build a maximum of 14 luxury houses and 20 standard houses. Determine the number of luxury and standard houses the developer must build to maximize his profit.

Bakery Optimization:

A bakery produces two types of bread: whole wheat and multigrain. Each loaf of whole wheat bread yields a profit of $3, while each loaf of multigrain bread yields a profit of $4. The bakery has 130 pounds of flour and 96 pounds of grains available. Whole wheat bread requires 3 pounds of flour and 2 pounds of grains per loaf, while multigrain bread requires 2 pounds of flour and 4 pounds of grains per loaf.

How many loaves of each type should the bakery produce to maximize its profit?

Cosmetology Service Pricing:

A beauty salon offers two types of services: haircuts and manicures. Each haircut generates a profit of $45, while each manicure generates a profit of $35. The salon has a time constraint and can only serve a maximum of 30 clients per day for every 12 hour day. Haircuts require 30 minutes per client, while manicures require 20 minutes per client. How many haircuts and manicures should the salon schedule per day to maximize its daily profit?

Car Tinting Cost Optimization:

A small car customization business wants to minimize the cost of window tinting for different car types. The business offers window tinting services for three car types: Sedan, and Truck. The business has the following constraints: Window tinting for a Sedan costs $124 per window, and for a Truck it costs $168 per window. A Sedan has a minimum of 5 windows to tint, and Truck has a minimum of 7 windows. The business has a total of 42 windows available for tinting. Determine how many windows to tint for each car type that will minimize the cost for the business to save on cost of materials.

Equine Science Breeding Optimization:

A horse breeding farm wants to maximize the profit from breeding and selling horses. The farm has limited resources and needs to decide how many horses of different breeds to breed. Breeding a Thoroughbred horse generates a profit of $40,000 per horse, while breeding a Quarter Horse generates a profit of $3,000 per horse. Breeding a Thoroughbred horse requires 2 stalls, while breeding a Quarter Horse requires 1 stall, and the farm has a total of 16 stalls. The farm can breed a maximum of 19 Thoroughbred horses and 12 Quarter Horses. Use linear programming to determine the number of Thoroughbred and Quarter Horses to breed that maximizes the profit.

Oilfield Rig Production Scheduling:

An oilfield company wants to maximize the production of both oil and natural gas from different wells while considering the resource limitations. The company has a limited number of drilling rigs and workers and needs to decide how many wells to drill for each resource. The company has the following constraints: Due to costs we can only have 22 rigs operating per month. Each well requires a team of 5 workers to operate, and the company has a maximum of 100 workers available. Each oil well generates a profit of $2 million, and each natural gas well generates a profit of $1.5 million. The company has a target of drilling a minimum of 5 oil wells and 8 natural gas wells.

Formulate a linear programming problem to determine the number of oil wells and natural gas wells to drill that maximizes the total profit while considering the limitations on drilling rigs, workers, and the minimum well requirements.

Kindly use the format below

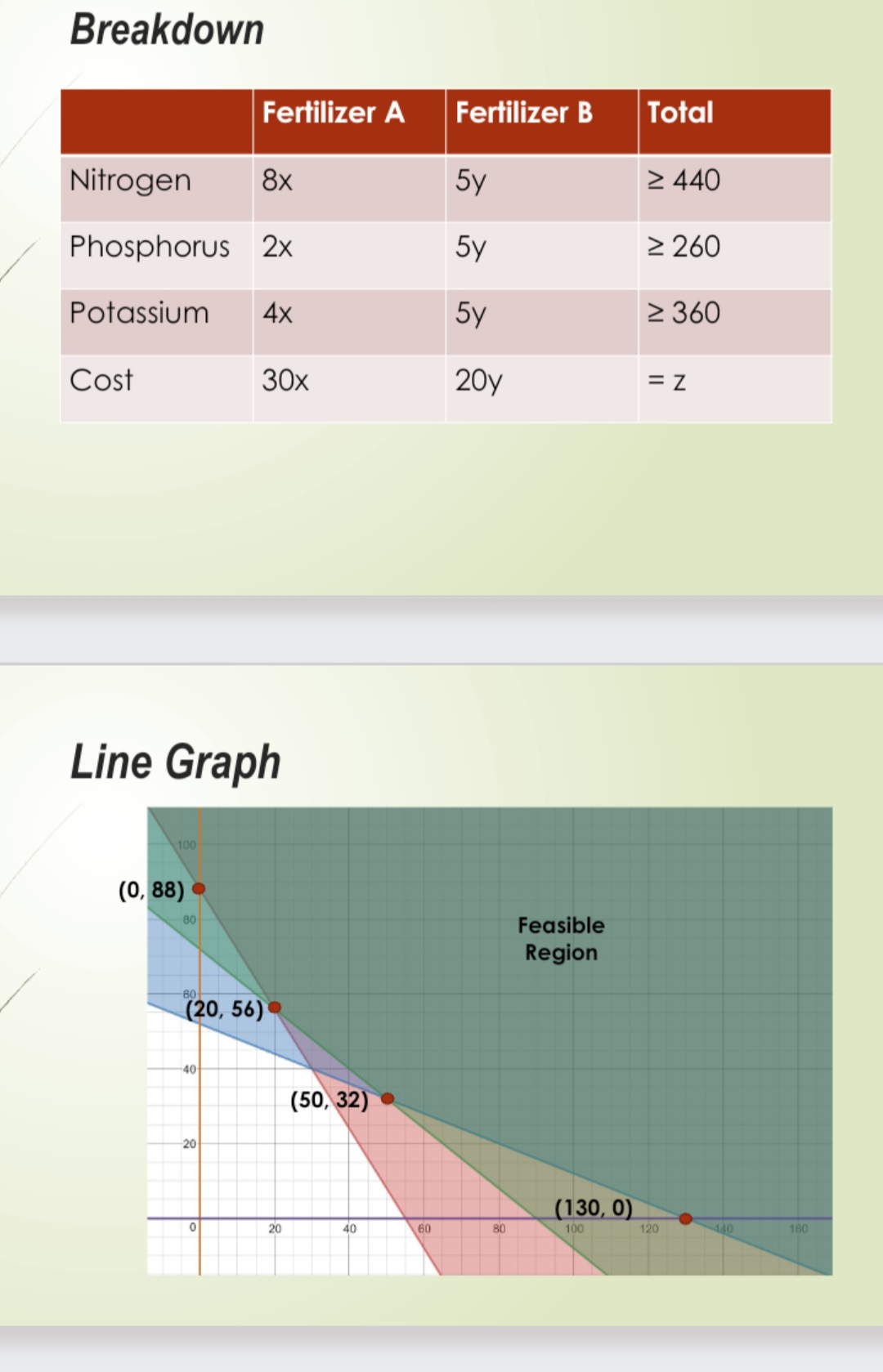
Business Math Project Question 7 FERTILIZERS - A farmer uses two types of fertilizers. A 50-lb bag of Fertilizer A contains 8 lb of nitrogen, 2 lb of phosphorus, and 4 lb of potassium. A 50-lb bag of Fertilizer B contains 5 lb each of nitrogen, phosphorus, potassium. The minimum requirements for a field are 440 lb of nitrogen, 260 lb of phosphorus, and 360 lb of potassium. If a 50-lb bag of Fertilizer A costs $30 and a 50-lb bag of Fertilizer B costs $20, find the amount of each type of fertilizer the farmer should use to minimize his cost while still meeting the minimum requirements. What is the minimum cost? OBreakdown Fertilizer A Fertilizer B Total Nitrogen 8x 5y 2 440 Phosphorus 2x 5y 2 260 Potassium 4x 5y 2 360 Cost 30x 20y = Z Line Graph 100 (0, 88) . 80 Feasible Region (20, 56) . 40 (50, 32) 20 (130, 0) 20 40 60 80 100 120 140 160Intersection Points plugged into cost (20,56) 30x+20y= 1720 (50,32) 30x+20y= \" (0,88) 30x+20y= 1760 (130,0) 30x+20y= 3900 Answer = Minimum cost: $1720 meaning 20lbs of Fertilizer A & 56lbs from Fertilizer B Minimizing cost is a necessary factor when it comes to agriculture due to the fact that fertilizer prices are becoming a consistent factor in annual production budgets. Deficiencies can be costly. = Farmers need to fine-tune operations to make certain their fertility prograr are as efficient as possible. |1 O &lt