math 79 linear algebra

Please solve the questions correctly. Thank you.

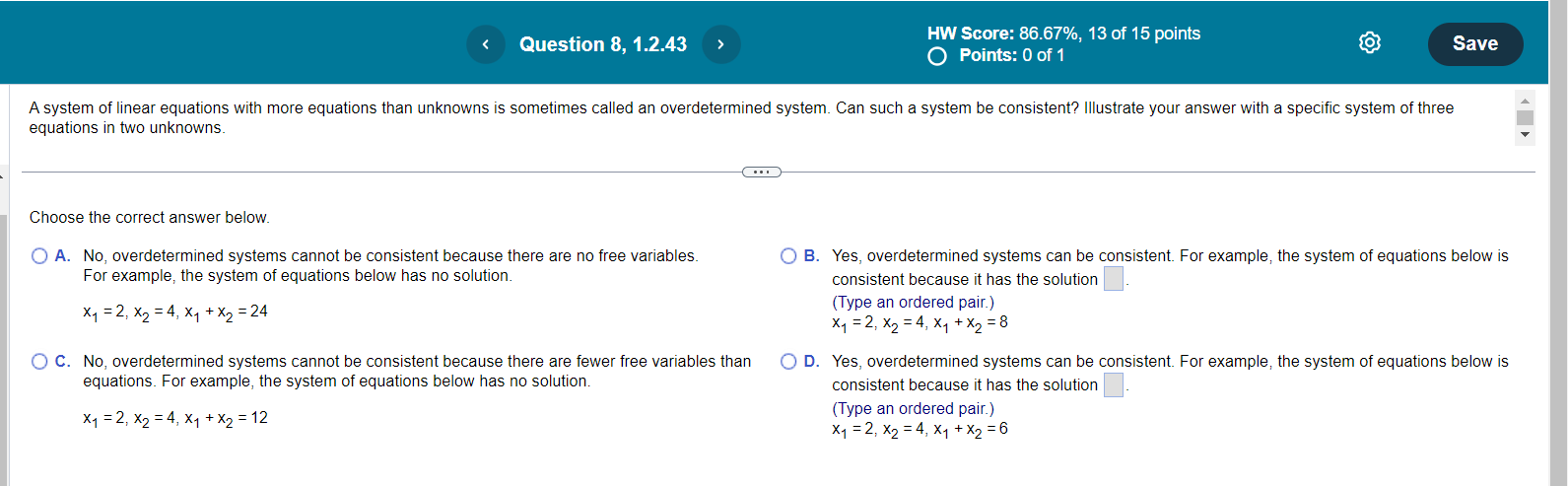
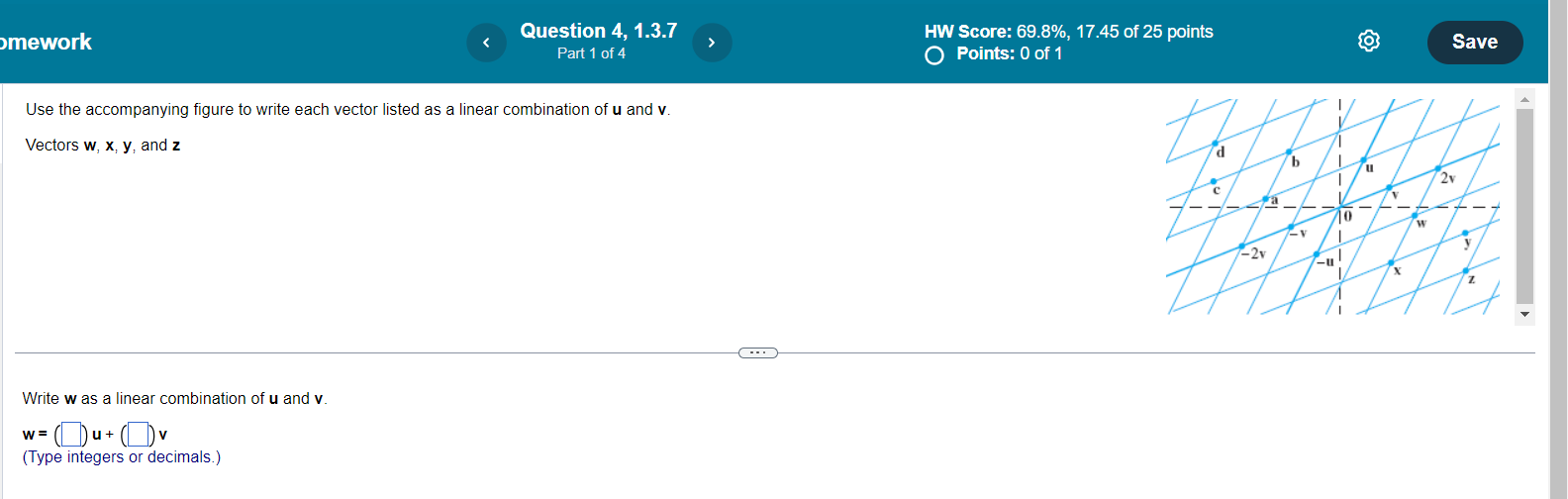
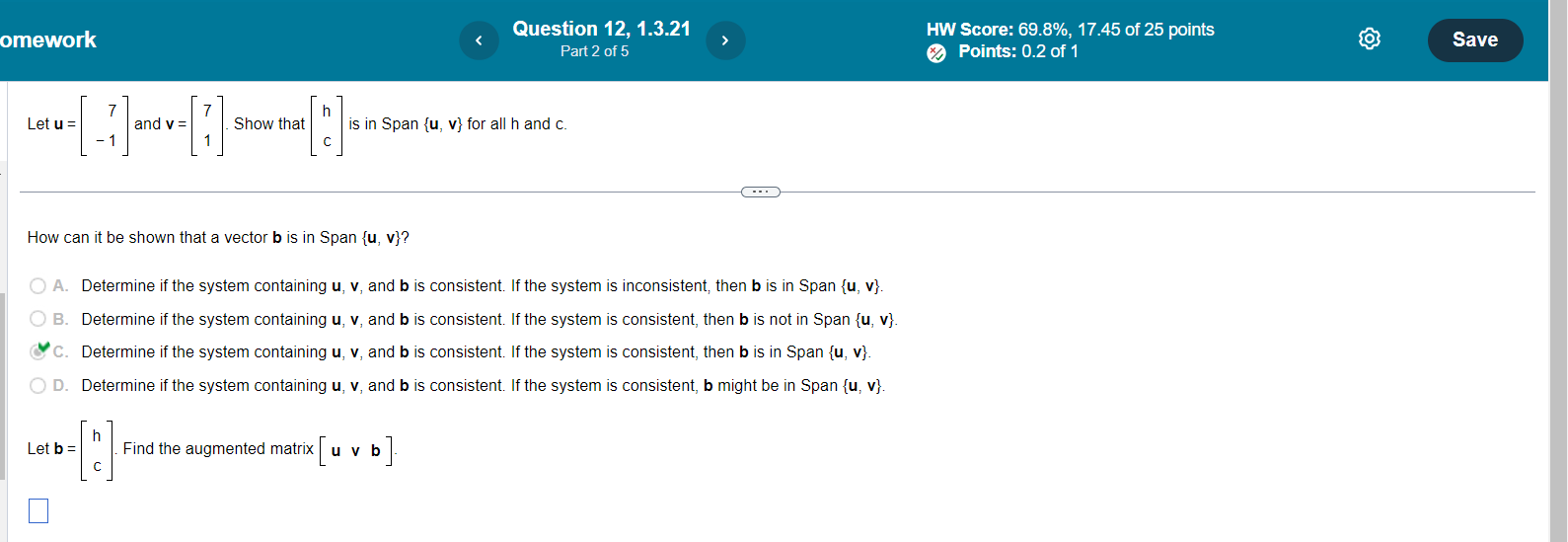
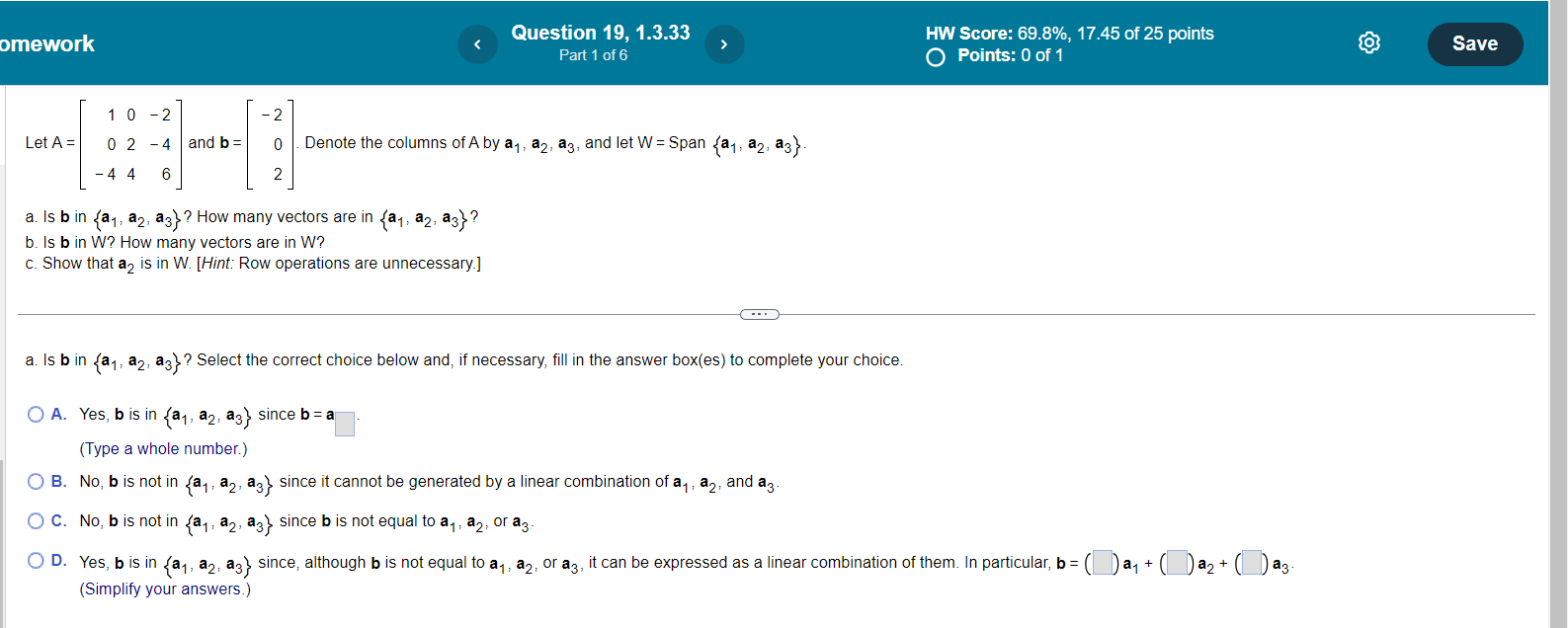
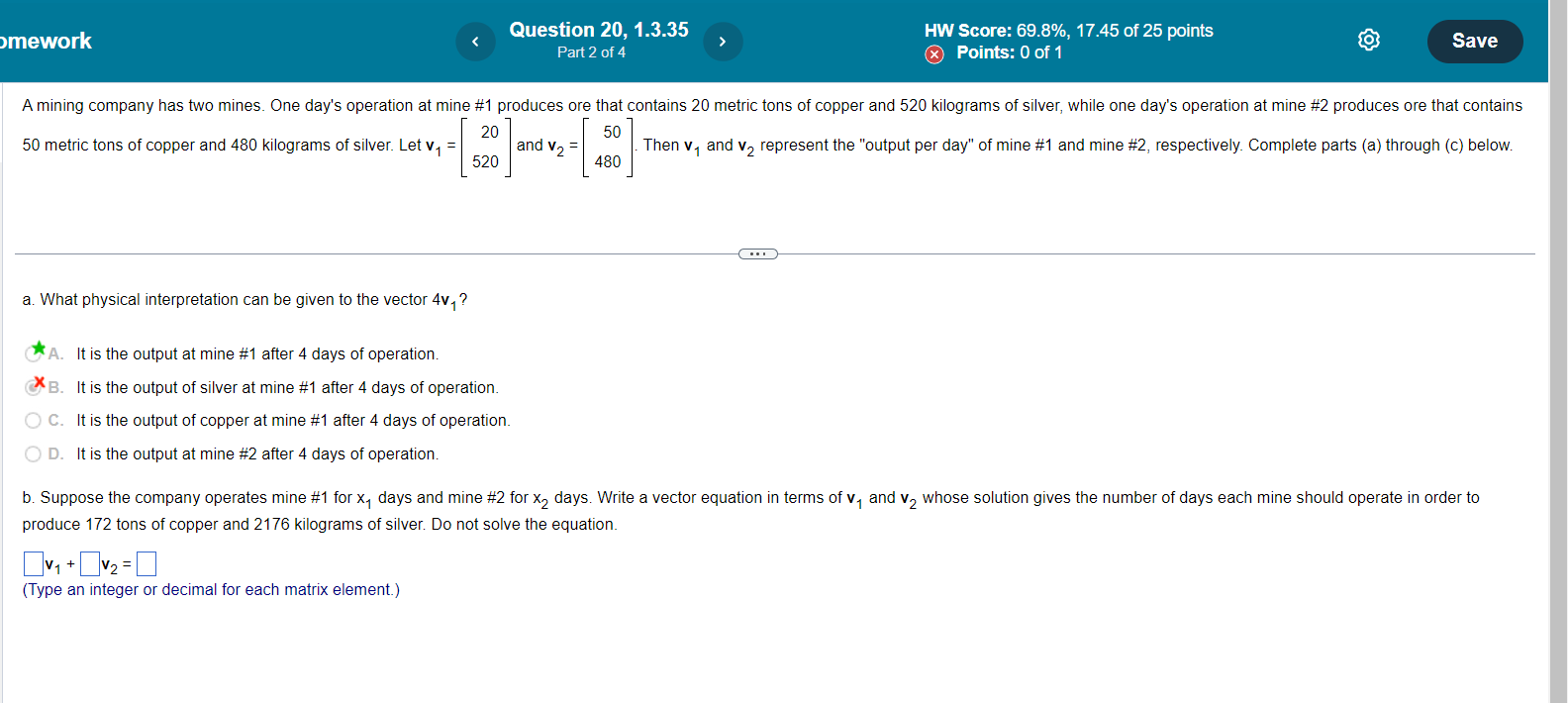
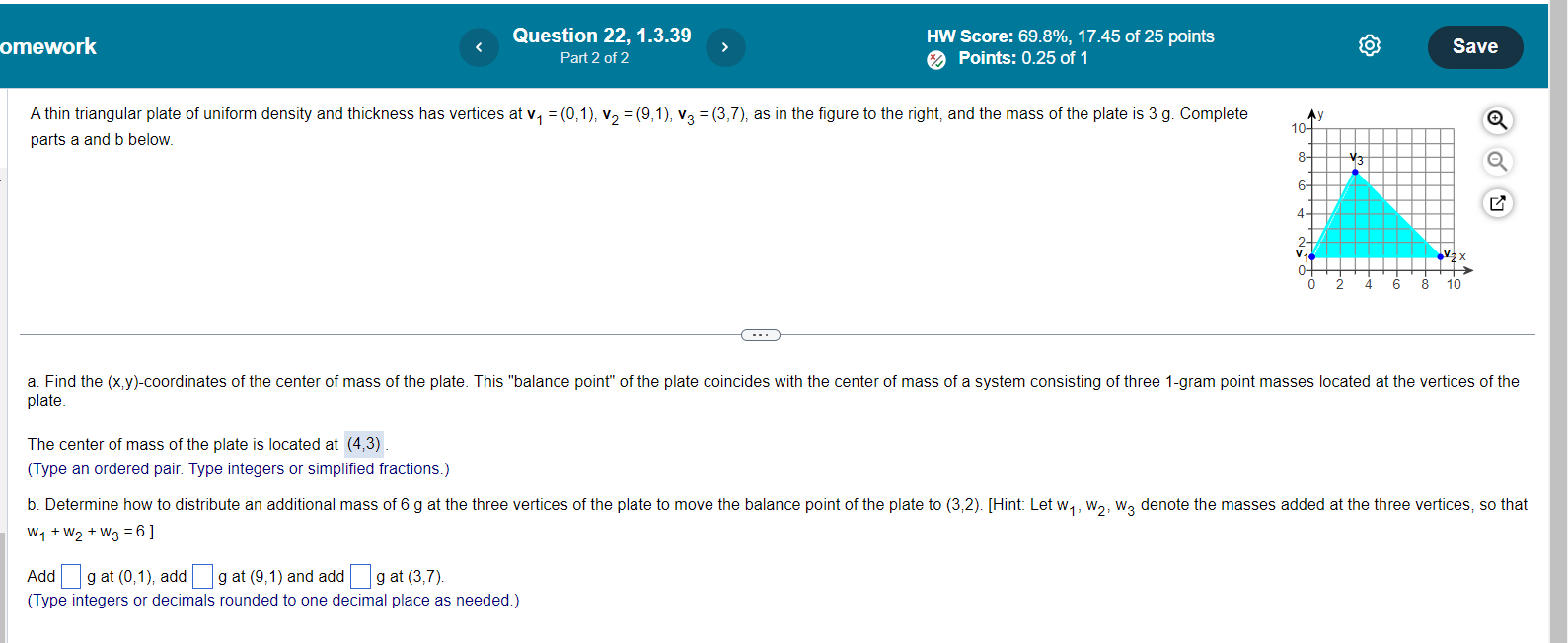
Question 8, 1.2.43 HW Score: 86.67%, 13 of 15 points Save O Points: 0 of 1 A system of linear equations with more equations than unknowns is sometimes called an overdetermined system. Can such a system be consistent? Illustrate your answer with a specific system of three equations in two unknowns. Choose the correct answer below. O A. No, overdetermined systems cannot be consistent because there are no free variables. O B. Yes, overdetermined systems can be consistent. For example, the system of equations below is For example, the system of equations below has no solution. consistent because it has the solution X1 = 2, X2 = 4, X1 + X2 = 24 (Type an ordered pair.) Xy = 2, X2 = 4, X1 + X2 = 8 O C. No, overdetermined systems cannot be consistent because there are fewer free variables than O D. Yes, overdetermined systems can be consistent. For example, the system of equations below is equations. For example, the system of equations below has no solution. consistent because it has the solution X1 = 2, X2 = 4, X1 + X2 = 12 (Type an ordered pair.) X1 = 2, X2 = 4, X1 + X2 = 6mework Question 4, 1.3.7 HW Score: 69.8%, 17.45 of 25 points Part 1 of 4 O Points: 0 of 1 Save Use the accompanying figure to write each vector listed as a linear combination of u and v. Vectors w, x, y, and z -2v Write w as a linear combination of u and v. w = ( )u + () v (Type integers or decimals.)omework Question 12, 1.3.21 HW Score: 69.8%, 17.45 of 25 points Save Part 2 of 5 Points: 0.2 of 1 [ : Janov- [:] snowman [ a is in Span {u, v} for all h and c. How can it be shown that a vector b is in Span {u, v}? O A. Determine if the system containing u, v, and b is consistent. If the system is inconsistent, then b is in Span {u, v}. O B. Determine if the system containing u, v, and b is consistent. If the system is consistent, then b is not in Span {u, v}. C. Determine if the system containing u, v, and b is consistent. If the system is consistent, then b is in Span {u, v}. O D. Determine if the system containing u, v, and b is consistent. If the system is consistent, b might be in Span {u, vi}. Letb = . Find the augmented matrix u v b .omework Question 19, 1.3.33 HW Score: 69.8%, 17.45 of 25 points Save Part 1 of 6 Points: 0 of 1 10 -2 - 2 Let A = 02 -4 and b = O Denote the columns of A by a1, a2, a3, and let W = Span {a1, a2, a3} -4 4 6 N a. Is b in {a1, a2, a3) ? How many vectors are in {ay, a2, a3)? b. Is b in W? How many vectors are in W? c. Show that a2 is in W. [Hint: Row operations are unnecessary.] - . . a. Is b in {a1, a2, a3) ? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. Yes, b is in {a1, a2, a3) since b = a (Type a whole number.) O B. No, b is not in fay, a2, age since it cannot be generated by a linear combination of a, , a2, and ag O C. No, b is not in {ay, a2, a3) since b is not equal to a,, a2, or a3 O D. Yes, b is in fay, a2, age since, although b is not equal to ay, a2, or ag, it can be expressed as a linear combination of them. In particular, b = ( ) a, + ( )a2 + ( )as (Simplify your answers.)mework Question 20, 1.3.35 HW Score: 69.8%, 17.45 of 25 points Save Part 2 of 4 x Points: 0 of 1 A mining company has two mines. One day's operation at mine #1 produces ore that contains 20 metric tons of copper and 520 kilograms of silver, while one day's operation at mine #2 produces ore that contains 20 50 50 metric tons of copper and 480 kilograms of silver. Let v, = and V, = Then v, and v2 represent the "output per day" of mine #1 and mine #2, respectively. Complete parts (a) through (c) below. 520 480 a. What physical interpretation can be given to the vector 4v, ? A. It is the output at mine #1 after 4 days of operation. XB. It is the output of silver at mine #1 after 4 days of operation. O C. It is the output of copper at mine #1 after 4 days of operation. O D. It is the output at mine #2 after 4 days of operation. b. Suppose the company operates mine #1 for x, days and mine #2 for X2 days. Write a vector equation in terms of v, and v2 whose solution gives the number of days each mine should operate in order to produce 172 tons of copper and 2176 kilograms of silver. Do not solve the equation. v1 + v2 = 0 (Type an integer or decimal for each matrix element.)omework Question 22, 1.3.39 HW Score: 69.8%, 17.45 of 25 points Part 2 of 2 Save Points: 0.25 of 1 A thin triangular plate of uniform density and thickness has vertices at v, = (0,1), V2 = (9,1), V3 = (3,7), as in the figure to the right, and the mass of the plate is 3 g. Complete 10- parts a and b below. V/3 10 . . . a. Find the (x,y)-coordinates of the center of mass of the plate. This "balance point" of the plate coincides with the center of mass of a system consisting of three 1-gram point masses located at the vertices of the plate. The center of mass of the plate is located at (4,3). (Type an ordered pair. Type integers or simplified fractions.) b. Determine how to distribute an additional mass of 6 g at the three vertices of the plate to move the balance point of the plate to (3,2). [Hint: Let w1, W2, Wg denote the masses added at the three vertices, so that W 1 + W2 + W3 = 6.] Add g at (0,1), add |g at (9,1) and add g at (3,7). (Type integers or decimals rounded to one decimal place as needed.)