math 79 linear algebra

Please solve the questions correctly. Thank you.

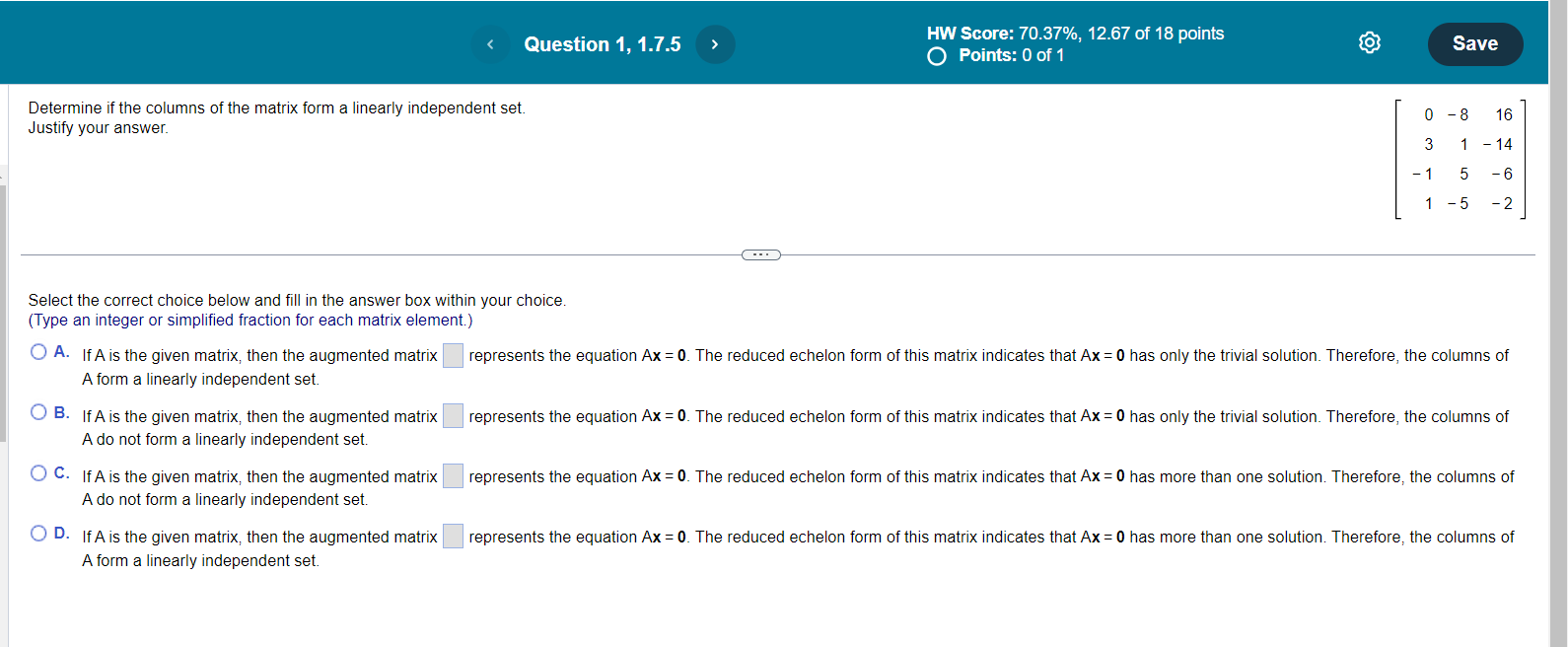
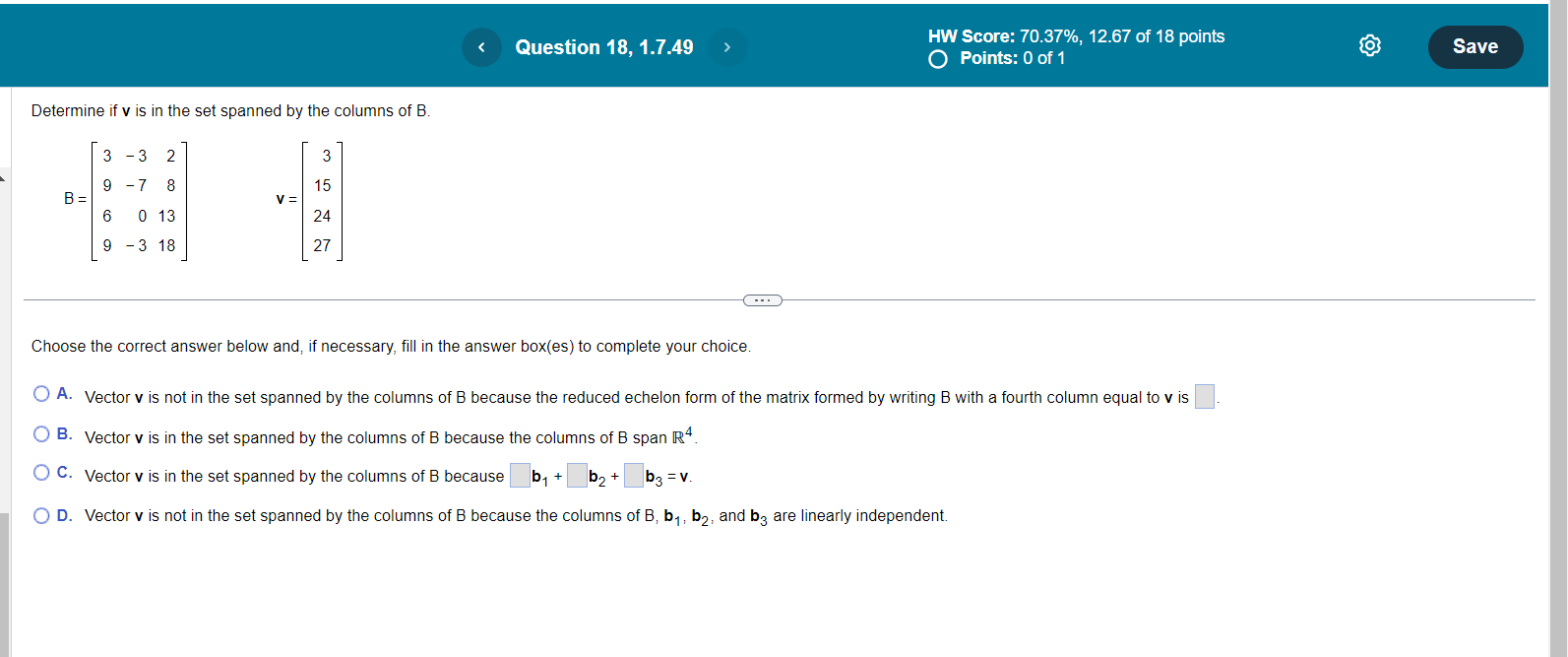
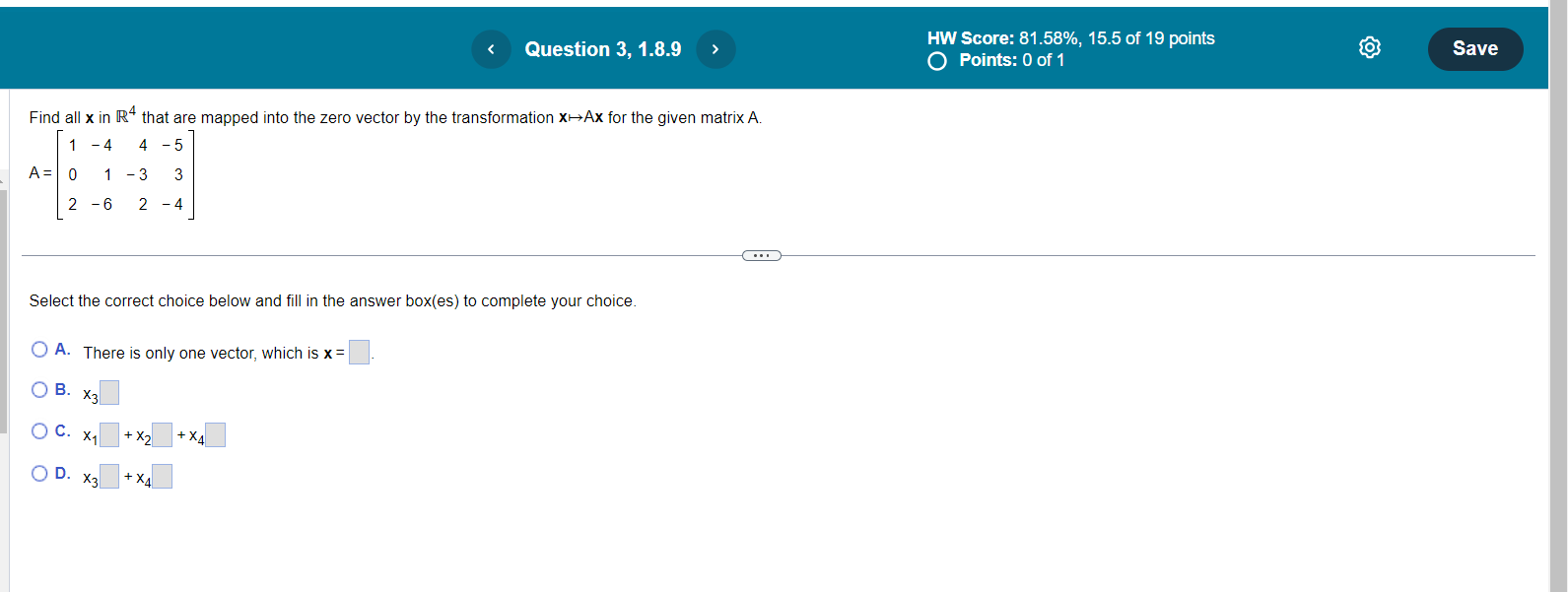
Question 1, 1.7.5 HW Score: 70.37%, 12.67 of 18 points Save O Points: 0 of 1 Determine if the columns of the matrix form a linearly independent set. 0 - 8 16 Justify your answer. 3 1 - 14 - 1 5 - 6 1 - 5 . . . Select the correct choice below and fill in the answer box within your choice. (Type an integer or simplified fraction for each matrix element.) A. If A is the given matrix, then the augmented matrix represents the equation Ax = 0. The reduced echelon form of this matrix indicates that Ax = 0 has only the trivial solution. Therefore, the columns of A form a linearly independent set. O B. If A is the given matrix, then the augmented matrix represents the equation Ax = 0. The reduced echelon form of this matrix indicates that Ax = 0 has only the trivial solution. Therefore, the columns of A do not form a linearly independent set. O C. If A is the given matrix, then the augmented matrix represents the equation Ax = 0. The reduced echelon form of this matrix indicates that Ax = 0 has more than one solution. Therefore, the columns of A do not form a linearly independent set. O D. If A is the given matrix, then the augmented matrix represents the equation Ax = 0. The reduced echelon form of this matrix indicates that Ax = 0 has more than one solution. Therefore, the columns of A form a linearly independent set.