MATLAB:

1. Construct an interpolating polynomial that approximates the function

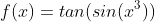on the domain [0, 3].

You can use any method to compute the polynomial.

2. The Matlab command x0=3*(0:(n-1))/(n-1); defines n equally-spaced base points in the interval [0, 3]. Take y0 values from the function f(x) at these x0 coordinates, using exact values from Matlabs trig functions. Find the degree n ? 1 interpolating polynomial Pn?1(x) that passes through the n points. Plot the actual f(x) versus Pn?1(x) on [0, 3] for n = 7. (Use a grid of width 0.01 or less to get a good plot.) Include the interpolating points, plotted as circles. In a separate figure, plot the interpolation error |f(x)?P6(x)| on [0, 3], using Matlabs semilogy command. Estimate the maximum interpolation error on the domain [0, 3].

3. How small can you make the maximum interpolation error on the domain [0, 3]? Find the n that makes it as small as possible. For this n, show the same two plots as in Step 1, the interpolation plot and the semilog interpolation error plot. Where along the interval [0, 3] is the error typically the largest?

4. Change the base points from equally-spaced to the Chebyshev points on [0, 3], and redo Step 2. Show the same two plots for your best n. You can replace the command above by the Matlab command x0=3/2+3/2*cos((1:2:2*n-1)*pi/(2*n)); to use the Chebyshev points. 4. What can you say about the comparison between interpolation with equally-spaced base points (Step 2) and Chebyshev points (Step 3)? 5. Why do you think the error eventually gets larger if you continue to increase n? If you make n very large you should see some Warnings in the Matlab command line, what do you think is causing these?

f(x) = tan sin(73) f(x) = tan sin(73)