MATLAB function help

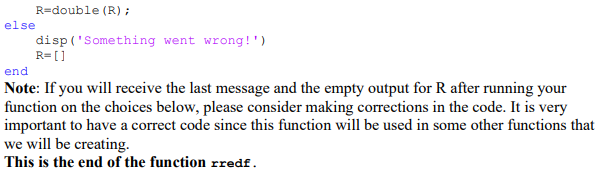
In this exercise you will write a function that reduces an m x n matrix A to the reduced echelon form by implementing the Row Reduction Algorithm in the way it will be outlined below. **Create a function in MATLAB that begins with: function R-rredf (A) format [m, n] =size (A); rankA=rank (A); A=sym (A); R=A; Notes: To increase accuracy in calculations, we work here with symbolic form of the input matrix A, A=sym (A), which we have assigned to the matrix R, and, after completing the Row Reduction algorithm on R, we will convert the output to a double precision matrix. We will follow the steps in the description of the Row Reduction Algorithm in Module 2 of Lecture Notes making some adjustments that will allow us to use the least possible number of row operations and obtain a function that can be used in other functions later on. **Continue your function with the line: *Forward Phase and begin with setting up a for loop with k=1:m that will work on submatrices of the consecutive iterations for R, which are formed by the rows of R in the range from k:m (and all columns), starting with the original matrix R (for k=1), and, for k>1, the submatrices of R are formed by deleting the top rows with the pivot positions that have been already completed after steps 1-3. This is described in Lecture 2 under Row Reduction Algorithm as Step 4: "4. Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it." Next, we will apply Steps 1-3 of the Row Reduction Algorithm to submatrices within the loop: **First, output the index of the left-most non-zero column (you can use command any () here), which is a pivot column and the pivot position is on its top. **Then, to select a non-zero entry in a pivot column that will be a pivot, output the index of the row with the largest by absolute value entry in the column (you can use here the MATLAB function [~, ]= max (abs ())), and, if that entry is not in the pivot position, use row interchanging operation to move it into the pivot position - this is called partial pivoting (see Numerical Note on Page 17 of textbook). **If a consecutive submatrix has more than one row (k1), create zeros above the pivot using row replacement operation: first, output the factor r that is used in the formula for the row replacement when the row is replaced with the sum of itself and r-multiple of the row with the pivot, and, then, place the command that will do row replacement using scalar r - please remember that your pivot here is the number 1. **After completing a consecutive row, place the following command into your code: R=closetozeroroundoff (R, 7); This is the end of the "for" loop and the end of the Backward Phase. Note: Suppress all intermediate outputs in the Row Reduction Algorithm. **After you completed Row Reduction Algorithm, output and display your matrix R as below: disp('the constructed matrix R is') disp (double (R)) Next, verify that R is, indeed, the reduced echelon form of A. Proceed as follows: **Place the following set of commands into your code: rf=rref (A); if closetozeroroundoff (R-rf, 7) ==0 disp('R is the reduced echelon form of A') R=double (R) ; else disp('Something went wrong!') R= [] end Note: If you will receive the last message and the empty output for R after running your function on the choices below, please consider making corrections in the code. It is very important to have a correct code since this function will be used in some other functions that we will be creating. This is the end of the function rredf. In this exercise you will write a function that reduces an m x n matrix A to the reduced echelon form by implementing the Row Reduction Algorithm in the way it will be outlined below. **Create a function in MATLAB that begins with: function R-rredf (A) format [m, n] =size (A); rankA=rank (A); A=sym (A); R=A; Notes: To increase accuracy in calculations, we work here with symbolic form of the input matrix A, A=sym (A), which we have assigned to the matrix R, and, after completing the Row Reduction algorithm on R, we will convert the output to a double precision matrix. We will follow the steps in the description of the Row Reduction Algorithm in Module 2 of Lecture Notes making some adjustments that will allow us to use the least possible number of row operations and obtain a function that can be used in other functions later on. **Continue your function with the line: *Forward Phase and begin with setting up a for loop with k=1:m that will work on submatrices of the consecutive iterations for R, which are formed by the rows of R in the range from k:m (and all columns), starting with the original matrix R (for k=1), and, for k>1, the submatrices of R are formed by deleting the top rows with the pivot positions that have been already completed after steps 1-3. This is described in Lecture 2 under Row Reduction Algorithm as Step 4: "4. Cover (or ignore) the row containing the pivot position and cover all rows, if any, above it." Next, we will apply Steps 1-3 of the Row Reduction Algorithm to submatrices within the loop: **First, output the index of the left-most non-zero column (you can use command any () here), which is a pivot column and the pivot position is on its top. **Then, to select a non-zero entry in a pivot column that will be a pivot, output the index of the row with the largest by absolute value entry in the column (you can use here the MATLAB function [~, ]= max (abs ())), and, if that entry is not in the pivot position, use row interchanging operation to move it into the pivot position - this is called partial pivoting (see Numerical Note on Page 17 of textbook). **If a consecutive submatrix has more than one row (k1), create zeros above the pivot using row replacement operation: first, output the factor r that is used in the formula for the row replacement when the row is replaced with the sum of itself and r-multiple of the row with the pivot, and, then, place the command that will do row replacement using scalar r - please remember that your pivot here is the number 1. **After completing a consecutive row, place the following command into your code: R=closetozeroroundoff (R, 7); This is the end of the "for" loop and the end of the Backward Phase. Note: Suppress all intermediate outputs in the Row Reduction Algorithm. **After you completed Row Reduction Algorithm, output and display your matrix R as below: disp('the constructed matrix R is') disp (double (R)) Next, verify that R is, indeed, the reduced echelon form of A. Proceed as follows: **Place the following set of commands into your code: rf=rref (A); if closetozeroroundoff (R-rf, 7) ==0 disp('R is the reduced echelon form of A') R=double (R) ; else disp('Something went wrong!') R= [] end Note: If you will receive the last message and the empty output for R after running your function on the choices below, please consider making corrections in the code. It is very important to have a correct code since this function will be used in some other functions that we will be creating. This is the end of the function rredf