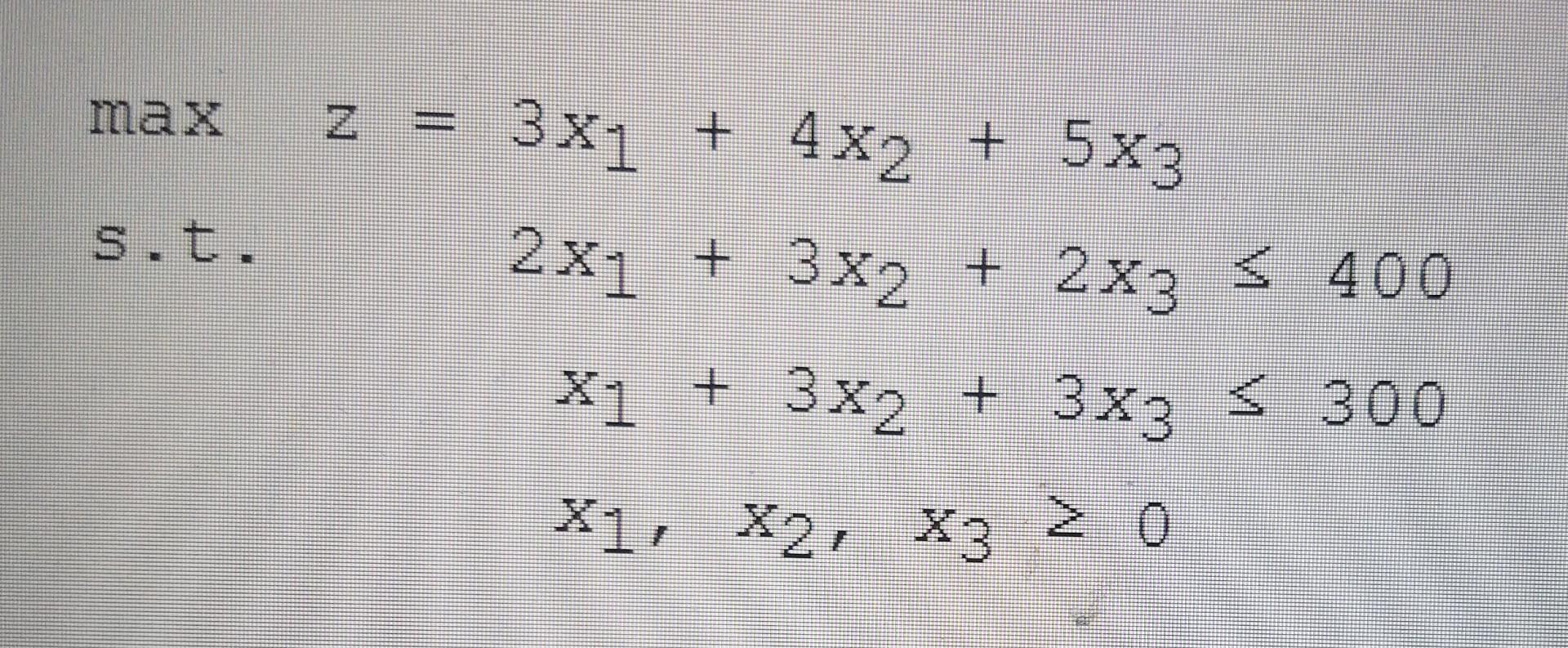
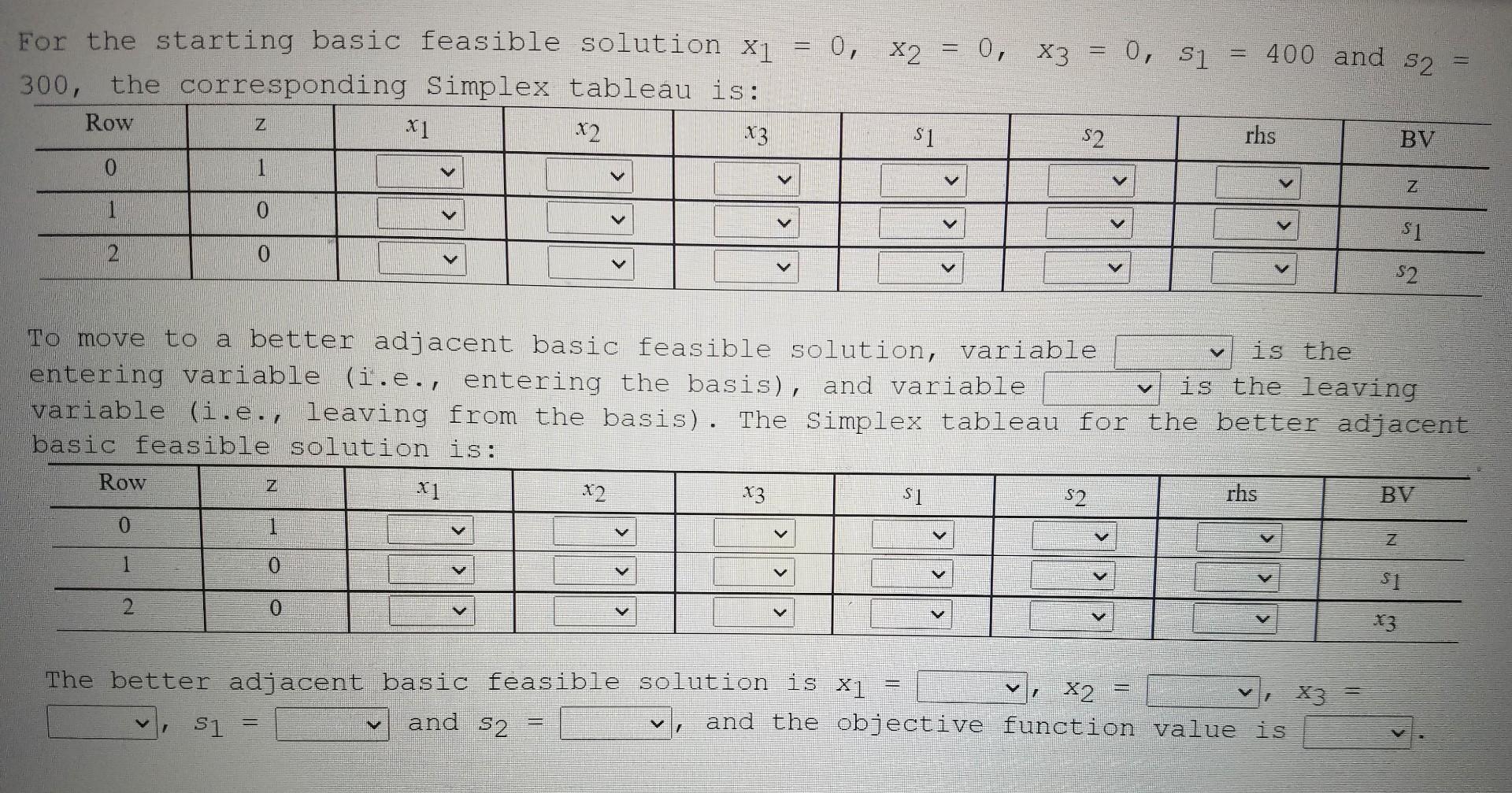
max E 3x1 + 4x2 + 5x3 s.t. 2x1 + 3x2 + 2x3 s 400 X1 + 3x2 + 3x3 3 300 X1 X2, X3 , , X2 = 0, X3 = 0, Si 400 and 52 For the starting basic feasible solution x1 = 0, 300, the corresponding Simplex tableau is: Row .12 X3 Z $1 rhs BV 0 1 V v Z 1 0 $1 2 0 V V 52 V V To move to a better adjacent basic feasible solution, variable is the entering variable (i.e., entering the basis), and variable is the leaving variable (i.e., leaving from the basis). The Simplex tableau for the better adjacent basic feasible solution is: Row si S2 rhs BV .X2 0 1 Z 1 0 2 0 The better adjacent basic feasible solution is X1 X2 and the objective function value is 7 ~, 51 = and S2 V 1