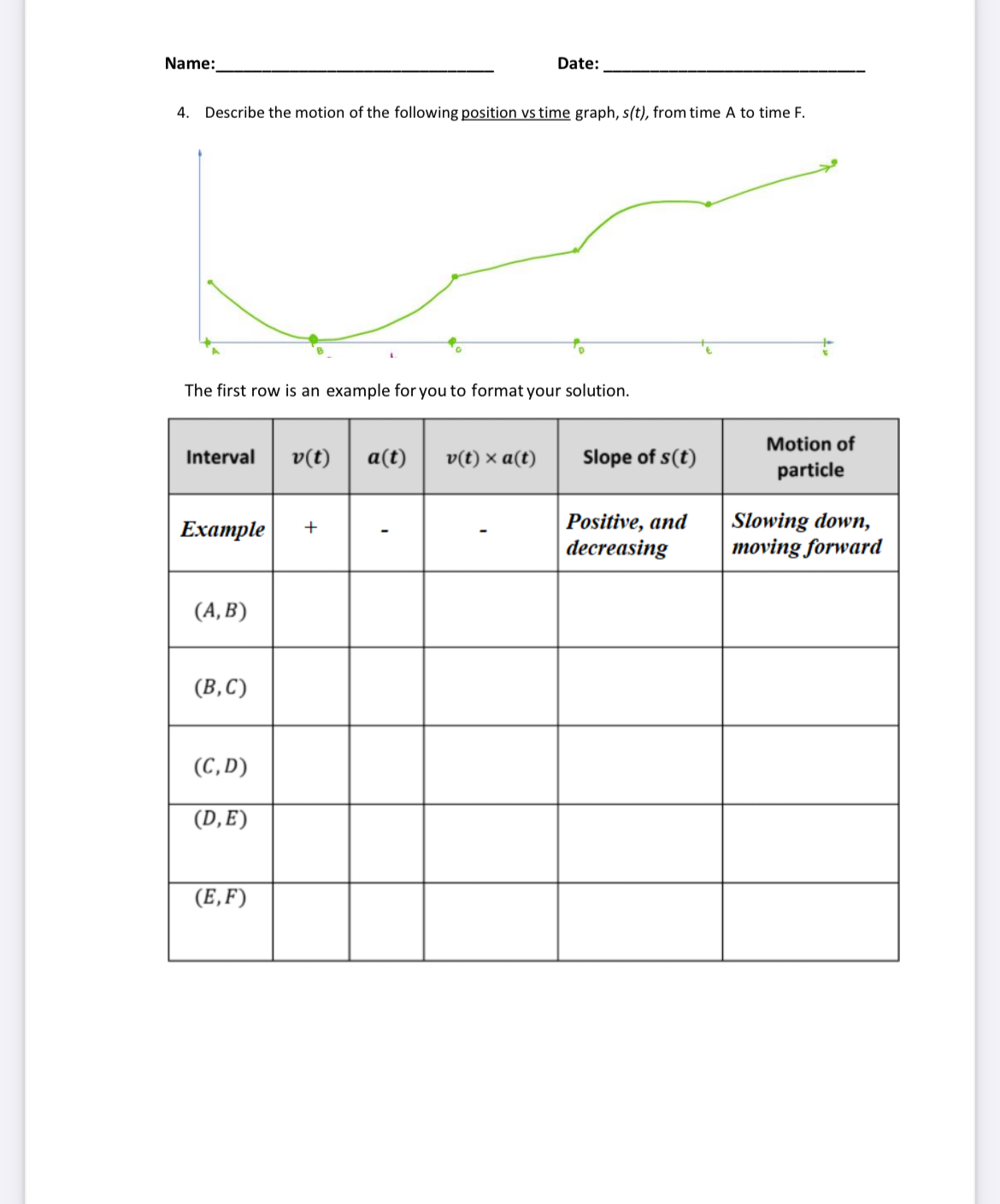
MCV4U - Unit 1: Derivative Rules Complete the Reference Declaration section below. If you used any references beyond the course text and lectures (such as other texts, discussions with colleagues or online resources), indicate this information in the space below. If you did not use any aids state this in the space provided. Declared references (Name, type of source/relation, etc...): Part A: Multiple Choice. Please answer the following MC questions on the GOOGLE FORM bubble sheet (not here). 1 For which value of x is the derivative of f(x) = (x 1)10 equal to zero? a.0 c.i2 b.1 d. 1 2 Determine f'(2) forf(x) = x2+ 4x 1 a.7 cyll b.8 d. 12 d 3 Determine the value of = for f(x) = x2(x2 4+ 1)?whenx =1 dx a.0 c. 12 b.4 d. 16 4 Which of the following functions has a derivative that is equal to 5 when x = 2? a. f (x) = 5x -3 c. h(x) = x3 - 1 b. g(x) = x2+ 1 d. k(x) x+1 5 For h(x) = () ", which expression represents h'(x) ? g(x) f (x) g' ( x ) f(x)g (x)-f (x)g(x) g(x)] b. : f (x)g'(x) [g(x)12 g(x)f (x)-g(x)f(x) d. [g(x)12 6 Under what condition is the tangent to f(x) at point a horizontal line? a. f'(a) > 0 c. f'(a) = 0 b. f'(a) 0 and b'(x) > 0 for all possible values of x. HINT: This may seem hard, but just try to think VERY carefully about your derivative rules here... a) If f{x) equals a(x) plus b(x), is it guaranteed that f{x) will always be increasing? Why or why not? b) If f{x) equals a(x) times b(x), is it guaranteed that f{x) will always be increasing? Why or why not? MCV4U Summer - July 2024 Monday Tuesday Wednesday Thursday Friday July 1 2 3 4 - 1 st Day of Class 5 A - Course Intro A -0.4 Limits & Continuity B -0.1 Avg Rates of Change B -1.1 Deriving Polynomials C-0.2 Inst Rates of Change C -1.2 Product Rule D -0.3 Newton's Quotient D - Unit 0 Assessment: Rates of Change 8 9 10 11 12 A - 1.3 Displacement, Velocity, & A -2.1 First Derivatives & Acceleration fing Rati actions A -UP essment: Increasing/Decreasing - 3.4 Deriving Exp F 8 - 1.4 Quotient Rule B - 2.2 Maximum & Minimums More Exper C - 1.5 Chain Rule C-2.3 Second Derivatives & frig Ful.c Actions, & D - 1.6 Applications: rig d Concavity Rate of Change D- 3.3 Trip D - Unit 1 Assessment: mal Modelling Deriv Derivatives for Midterms 15 16 17 18 19 A-Unit - 4.4 Physics Applicati C - 54 of Cross Prod hs of Plane of Planes Form ork Peri 22 23 24 25 26 A - 6.5 Intersection of 3D Lines A - Unit 6 Assessmom Lines an classes! Ace Work P D - Wor anod Have a great rest of D- Course Wrap Up