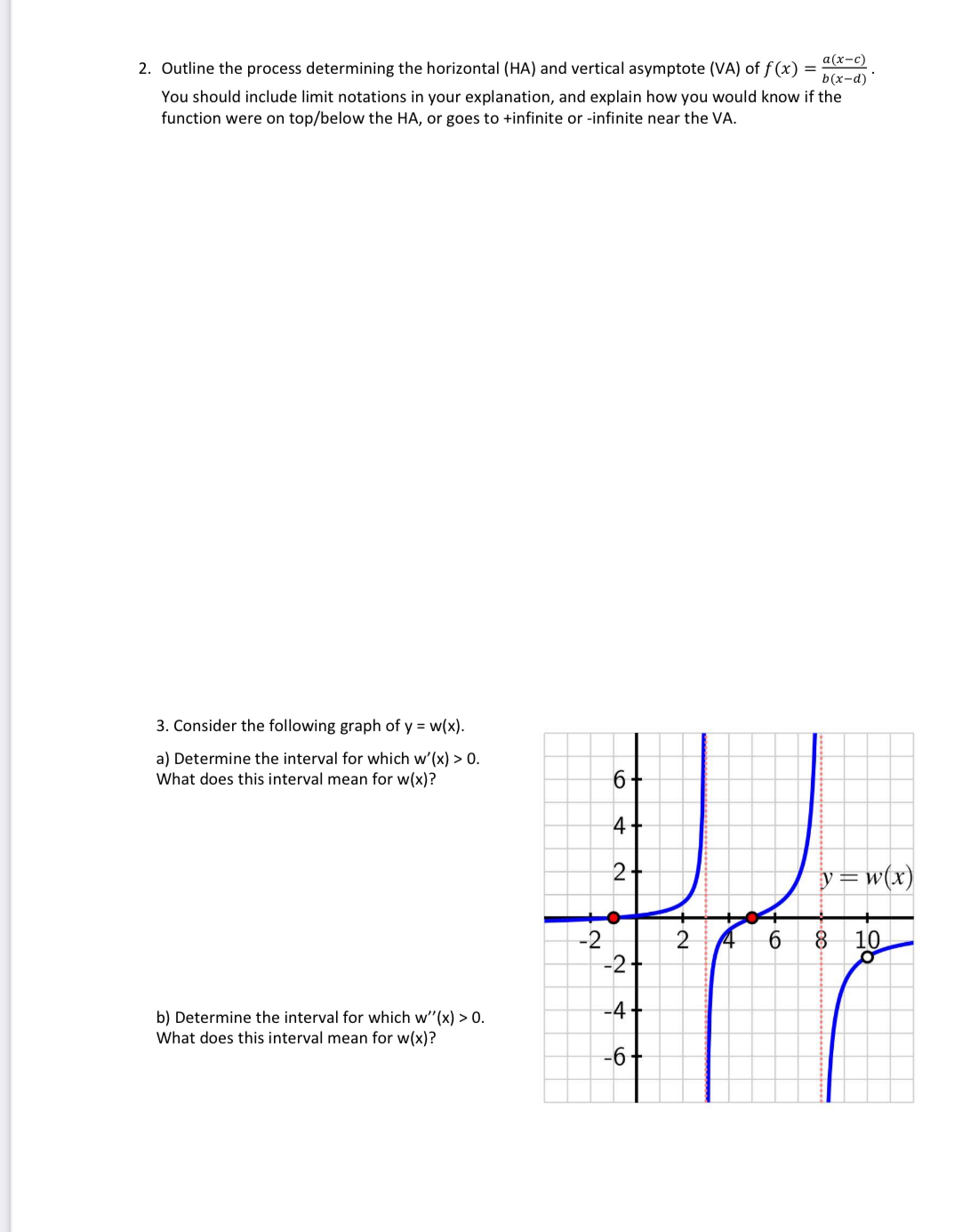
Name: Date: MCVA4U - Unit 2: Curve Sketching Complete the Reference Declaration section below. If you used any references beyond the course text and lectures (such as other texts, discussions with colleagues or online resources), indicate this information in the space below. If you did not use any aids state this in the space provided. Declared references (Name, type of source/relation, etc...): For all answers, please communicate as clearly and concisely as possible. Show all work! Refer to rubric for marking scheme. 1. In this unit, we discussed the existence of \"cusps\". Explain what cusps are, and why functions like f{x) = [x[ and f(x) = {x' e 22 e 8 said to be not differentiable at x = 0. a(x=c) b(x-d)" You should include limit notations in your explanation, and explain how you would know if the function were on top/below the HA, or goes to +infinite or -infinite near the VA. 2. Outline the process determining the horizontal (HA) and vertical asymptote (VA) of f(x) = 3. Consider the following graph of y = w(x). a) Determine the interval for which w'(x) > 0. What does this interval mean for w(x)? b) Determine the interval for which w"'(x) > 0. What does this interval mean for w(x)? 4. Consider the following function: fx)= 2 2+ D(x - 1) a) Find the 1%t and 2" derivatives. You may wish to use online tools to expand, simplify, refactor the numerator after applying quotient rule. b) Determine the followings characteristics of the function. -X and Y Intercepts -Any horizontal and vertical asymptotes -Critical points on f'(x) -Inflection points on f"(x)Name: Date: c) Draw a sign chart for function and use it to determine the shape of the function. d) Draw the function according to the results you obtained from parts a) to c). Label the local minima/maxima, axis intercepts, and any points of inflection found. 5. Determine the values of a, b, and c such that the graph of y = ax + bx + c has a local maximum at (3, 10) and a y-intercept at (0, 1). 6. Determine both the global minima and global maxima for the function: 2 -x f ( x ) = (S'S-]exA . I+ z*Tom is getting ready to leave his house at 10am. At the same time, Sam is 100 km south of Tom's house. If Tom leaves and moves at 5 km/h East, and Sam is moving towards Tom''s house at 8 km/h, find the time of day at which Tom and Sam are the closest. Assume that both would get tired and end their trip at 6pm. Hint 1: Try drawing a diagram for each of their paths. Pythagorean theorem may be useful here! Hint 2: Don't forget to check endpoints on restrictions! MCV4U Summer - July 2024 Monday Tuesday Wednesday Thursday Friday July 1 2 3 4 - 1 st Day of Class 5 A - Course Intro A -0.4 Limits & Continuity B -0.1 Avg Rates of Change B- 1.1 Deriving Polynomials C-0.2 Inst Rates of Change C-1.2 Product Rule D -0.3 Newton's Quotient D - Unit O Assessment: Rates of Change 8 9 10 11 12 A - 1.3 Displacement, Velocity, & A- 2.1 First Derivatives & A - 2.4 Deriving Rational Functions A - Unit 2 Assessment: A -3.4 De ions Acceleration Increasing/Decreasing B - 2.5 Curve Sketching Curve Sketching B- 35 M es 8 - 1.4 Quotient Rule B - 2.2 Maximum & Minimums C-2.6 Optimization B -3.1 Deriving Trig Functions C- ons, & C -1.5 Chain Rule C-2.3 Second Derivatives & D - 2.6 Optimization Cont. C-3.2 More Trig derivatives Im D - 1.6 Applications: Concavity D -3.3 Application of Trig DE Rate of Change D - Unit 1 Assessment: Derivatives Derivatives 15 16 17 18 A - Unit 3 A - 4.4 Physic ications .Dot act A -5.5 Cross Produ - 6 Transce Components 8-5.3 ions o -5.6 Application n of Cross Pr B -6.3 qua B-4 an Vectors Wertor Equation of Line ar Form C- D - Wor 10d itor ines classe b.t 6.8 In PI 6.8 Int. of 3 Cont Assessme C- ve a gi est of st O rio