Model Selection (if multiple predictor variables)

1. Consider all the predictor variables simultaneously. Based on the p-values of the slope coefficients, are any of these much less useful predictor variables for predicting the response variable (target)? Why or why not?
2. Based on the best subset analysis, which model do you recommend? Why?
3. Any collinearity problems? Why or why not?
4. What decision do you recommend to management based on these findings?

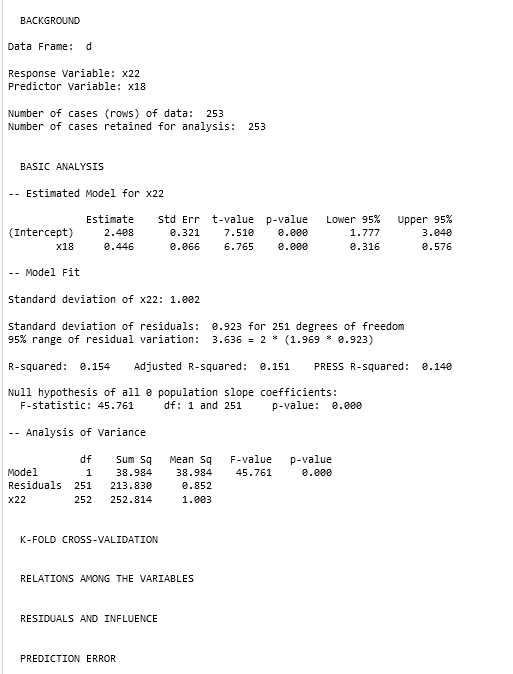
BACKGROUND Data Frame: d Response Variable: x22 Predictor Variable: x18 Number of cases (rows) of data: 253 Number of cases retained for analysis: 253 BASIC ANALYSIS Estimated Model for x22 Estimate Std Err t-value p-value Lower 95% Upper 95% (Intercept) 2.408 0. 321 7.510 1.777 3.840 x18 8.446 3.866 6.765 3. 316 8. 576 - - Model Fit Standard deviation of x22: 1.802 Standard deviation of residuals: @.923 for 251 degrees of freedom 95% range of residual variation: 3.636 = 2 $ (1.969 $ 0.923) R-squared: 0.154 Adjusted R-squared: 0.151 PRESS R-squared: 0.140 Null hypothesis of all @ population slope coefficients: F-statistic: 45.761 df: 1 and 251 p-value: 0.080 -- Analysis of Variance df sum 5q Mean 5q F-value p-value Model 38.984 38.984 45.761 0. 080 Residuals 251 213 . 838 8. 852 *22 252 252 . 814 1. 803 K-FOLD CROSS-VALIDATION RELATIONS AMONG THE VARIABLES RESIDUALS AND INFLUENCE PREDICTION ERROR