Question: Modern Algebra: Finitely generated abelian groups Exercise Il. Let (a,,.. , an) be a basis of a free abelian group A and B a subgroup

Modern Algebra: Finitely generated abelian groups

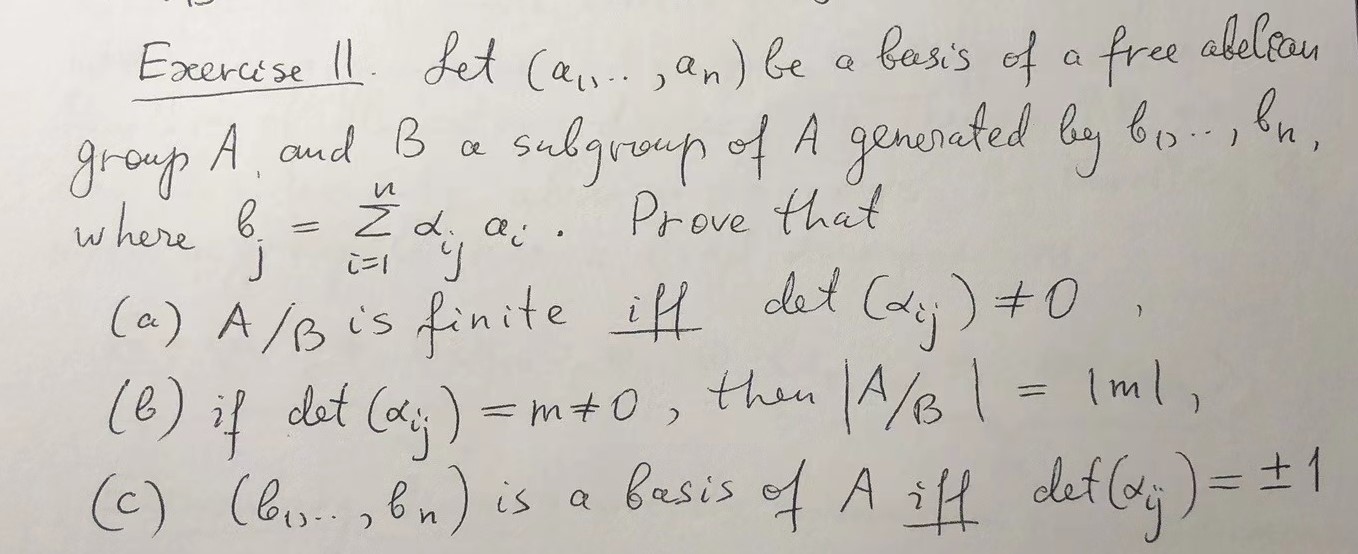
Exercise Il. Let (a,,.. , an) be a basis of a free abelian group A and B a subgroup of A generated by bis.., th, where 6. = Zda. Prove that C= 1 (a) A/ Bis finite iff det ( 2:; ) + 0 ( 8) if det (a; ) = mto , then | A/ B| = 1ml, ( c ) ( lis.. , bu ) is a basis of A iff def (dij ) = # 1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Modern Algebra: Finitely generated abelian groups Exercise 12. Let ( 91 , 2 2, (3, 24 ) be a basis of a free abelian group A, and Ba subgroup generated By 61, 62, 63 , where\f

Modern Algebra: Finitely generated abelian groups Exercise 10. Let A be a free abelian group with basis (a,, Q2, a3, 24). Denote by B the subgroup of A with generators bebz, by, By, where 6 = 12 a, +...

Modern Algebra: Finitely generated abelian groups Excercise I(a) Prove that a subgroup of n-generated abelian group is also in-generated. ( Hint : Use theorems ( and 3). ( 6) Give an example of a...

Modern Algebra: Finitely generated abelian groups 6 . Let G = H X H and 2 the diagonal of 6 : D = [ ( h, h) ThElly. Prove that Dis a subgroup of Gi which is normal in G off His an abelian group

Let G be a finite abelian group and x an element of maximal order. Show that (x) is a direct summand of G. Use this to obtain another proof of Theorem 2.1. Data from theore m 2.1 Every finitely...

Use the Krull-Schmidt Theorem to prove Theorems 2.2 and 2.6 (iii) for finite abelian groups. Data From Theorem 2.2 Every finitely generated abe/ian group G is (isomorphic to) a finite direct sum of...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Modern Algebra: Finitely generated abelian groups Exercise 15 Find the number of abelian groups (up to isomorphism ) of order (a) 400, ( 8) 210

Modern Algebra: Finitely generated abelian groups Please explain it clearly Exercise 13. How many distinct subgroups of order 10 are there in a non-cyclic abelian group of order 20

Modern Algebra: Finitely generated abelian groups Please prove it. Exercise are the groups KY, k,, and ZOZ 18 216 isomorphic

A man wants to help provide a college education for his young daughter. He can afford to invest $600/yr for the next 4 years, beginning on the girl's fourth birthday. He wishes to give his daughter...

In the scenario of Question 6.5.3, suppose the alternative hypothesis is H 1 : = 1 , for some particular value of 1 . How does the likelihood ratio test change in this case? In what way does the...

2. The thermometer was placed into a beaker of water that was exactly 56.3 C. Draw a diagram to show the reading on the thermometer. 27 26 25 Fig. 13.12

InvestmentUsefullifeEstimatedannualnetcashintiowsfor9yearsResidualvalueDepreciationmethodRequiredrateofreturnProposalX$870,0009years$105,000$68,000Straight-line19%ProposalY$456,0009years$75,000$Stragh...