Question: MODULE 1: Lesson 5 ASSIGNMENT Lesson 5: Inverse of a Relation The Module '1: Lesson hssignrnent is worth 16 marks. The value of each question
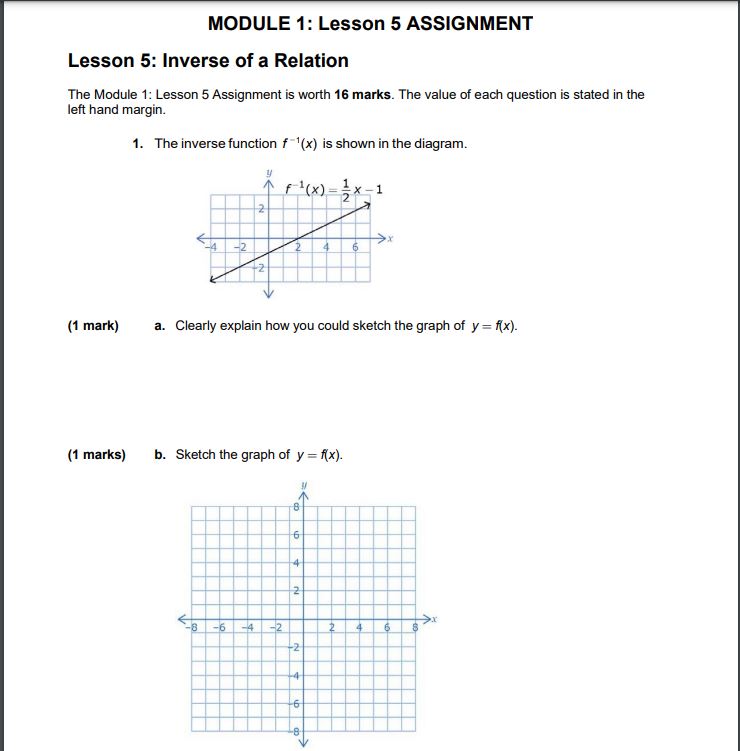

![f '{x} is shown in the diagram. r l{JrJ%xl {1 mark] 3.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666472f176d3e_057666472f161093.jpg)
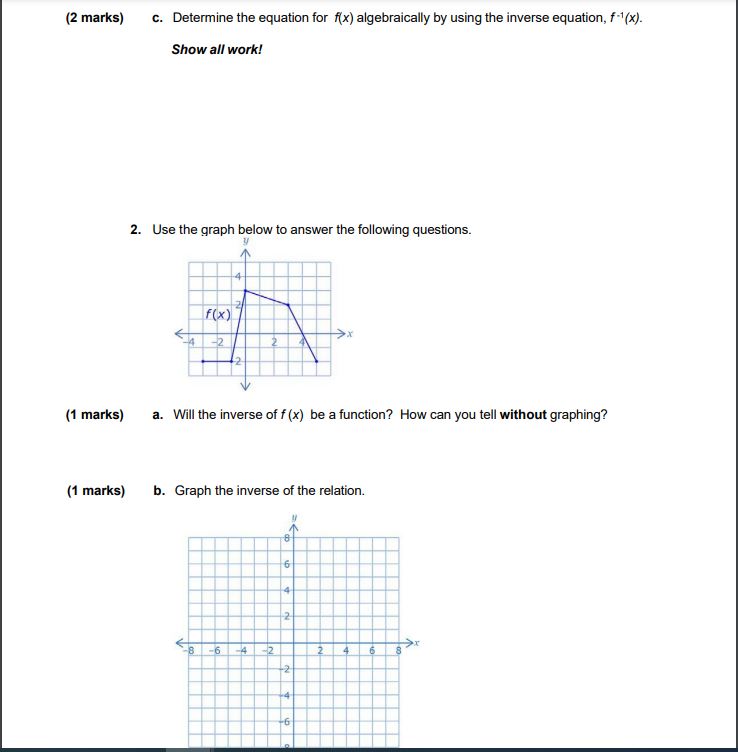
![{1 marks] in. Sketch the graph of y : x}. (2 marks)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666472f2086d0_057666472f1eafce.jpg)

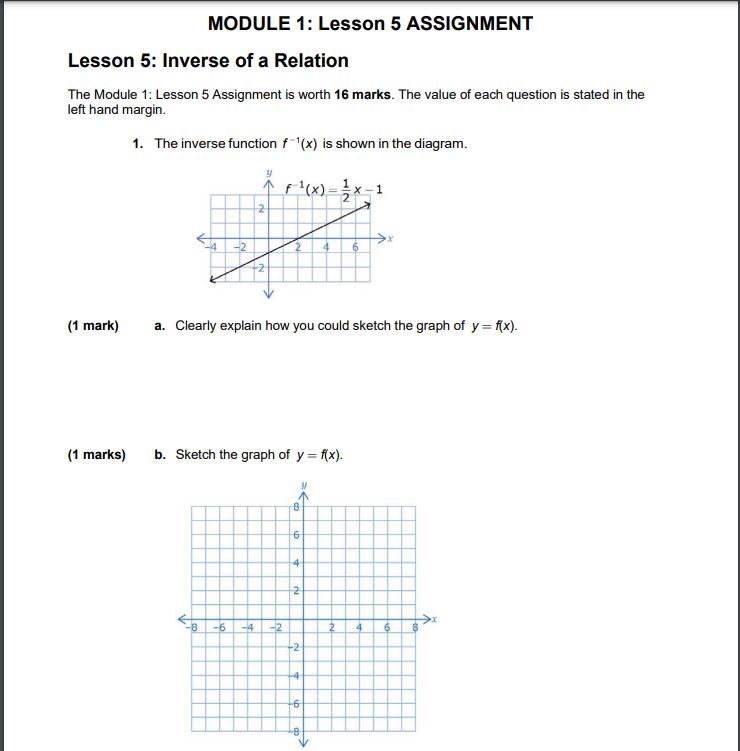
MODULE 1: Lesson 5 ASSIGNMENT Lesson 5: Inverse of a Relation The Module '1: Lesson hssignrnent is worth 16 marks. The value of each question is stated in the left hand margin. 1. Theirwerse funetien f '{x} is shown in the diagram. r l{JrJ%xl {1 mark] 3. Clearly explain haw you could sketch the graph at y : x}. {1 marks] in. Sketch the graph of y : x}. (2 marks) c. Determine the equation for f(x) algebraically by using the inverse equation, f-1(x). Show all work! 2. Use the graph below to answer the following questions. f(x (1 marks) a. Will the inverse of f (x) be a function? How can you tell without graphing? (1 marks) b. Graph the inverse of the relation. B -6{3 maria} c. Determine the domain and range for both x} and f 'lxj. Clearly.r label your answers. What are the similarities and differences between the domain and ranges for 1'fo and f "{1}? {1 mark} 3. Determine a mapping of the form (x. y} + t i for the inverse of a relation. Explain how 1vou determined this mapping. {2 marks} 4. a. Determine the inverse of x} : 2x2 + 4. Showr all work! {2 marks] b. What restrictions can we make to the domain of fix}, so that its inverse becomes a function? Explain why would these restrictions turn the inverse into a function?
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


