MP3.3. Strategy to solve KU=P

Note - there can be more than one pair of rows/columns to swap

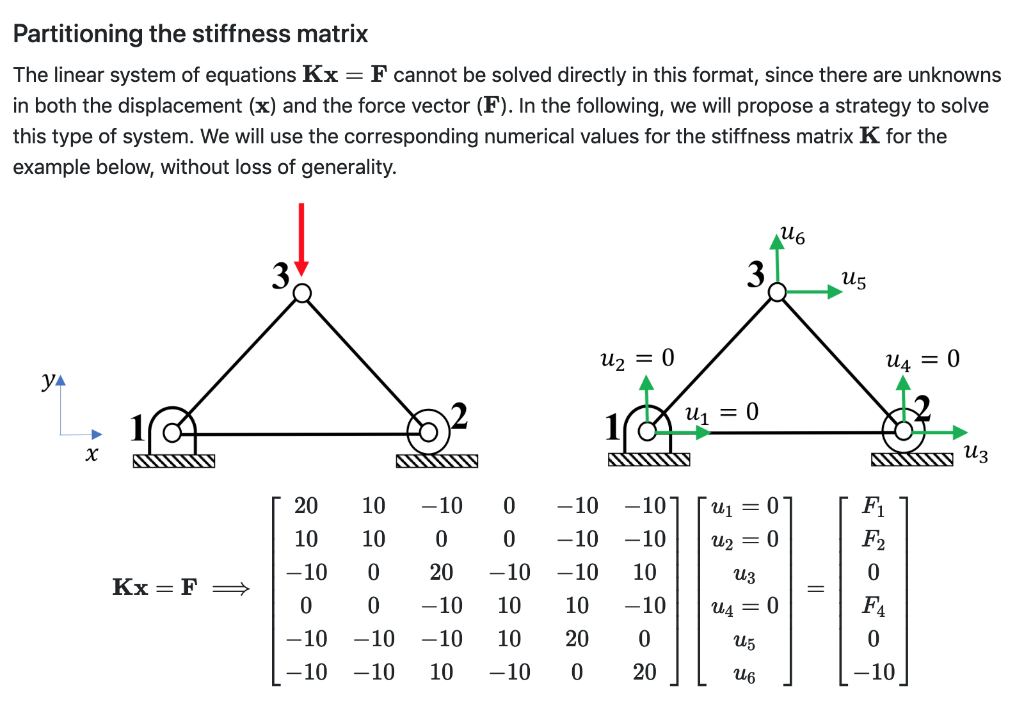
Partitioning the stiffness matrix The linear system of equations Kx- F cannot be solved directly in this format, since there are unknowns in both the displacement (x) and the force vector (F). In the following, we will propose a strategy to solve this type of system. We will use the corresponding numerical values for the stiffness matrix K for the example below, without loss of generality. 4 lu 20 10 10 10 0 10 0 0 10-10 | | u2=0 10 0 20 -10 -10 10 U3 10 10 10 10u40 10-10 -10 10 200 10-10 10 0 10 U5 10 0 20 Let's swap rows and columns 3 and 4, such that the known quantities "stay together". In general, rows and columns of K are swapped such that the equations associated with the nodes that have prescribed (known) displacements and unknown reaction forces are positioned in the first rows. 20 10 0 10 10 0 0 1O 10-10-101 -0 10-10u20 10 10 10 0 10-10 10 -10 200 10-10 -10 10 020 10 20 10 10 ul5 10 The two linear system of equations are equivalent. We will learn soon how to solve the system Ki- F in an efficient way. But first, how can we construct the matrix K if we have the matrix K? To accomplish this, we will provide the array equation_numbers which contains the order in which the displacements appear in the array x. For the example above, we have equation_numbers np.array([1,2,4,3,5,6]). Note that equation_numbers is 1-indexed In your code snippet, define the function swap_rows_columns, that takes as argument the matrix K and the array equation_numbers and returns the matrix K def swap_rows_columns (K, equation_numbers) # construct the matrix Khat return Khat The setup code provides the matrix K from the example above. You can use it for debugging purposes (since you know what K should look like), but we will test your function using different input arguments. The setup code provides the following variable(s) and/or function(s): Name Type 2d numpy array stiffness matrix corresponding to the example (to help debugging) Description equation_numbers d numpy array ordering of the displacements for partition Your code snippet should define the following variable(s) and/or function(s): Name swap_rows_columns Type unction swaps rows and columns of a matrix Description (1): In typical FEA algorithms, the matrix K is constructed directly, without the need of constructing the matrix K first. user_code.py 1 mport numpy as np 3- def swap_rows_columns(K, equation_numbers): Partitioning the stiffness matrix The linear system of equations Kx- F cannot be solved directly in this format, since there are unknowns in both the displacement (x) and the force vector (F). In the following, we will propose a strategy to solve this type of system. We will use the corresponding numerical values for the stiffness matrix K for the example below, without loss of generality. 4 lu 20 10 10 10 0 10 0 0 10-10 | | u2=0 10 0 20 -10 -10 10 U3 10 10 10 10u40 10-10 -10 10 200 10-10 10 0 10 U5 10 0 20 Let's swap rows and columns 3 and 4, such that the known quantities "stay together". In general, rows and columns of K are swapped such that the equations associated with the nodes that have prescribed (known) displacements and unknown reaction forces are positioned in the first rows. 20 10 0 10 10 0 0 1O 10-10-101 -0 10-10u20 10 10 10 0 10-10 10 -10 200 10-10 -10 10 020 10 20 10 10 ul5 10 The two linear system of equations are equivalent. We will learn soon how to solve the system Ki- F in an efficient way. But first, how can we construct the matrix K if we have the matrix K? To accomplish this, we will provide the array equation_numbers which contains the order in which the displacements appear in the array x. For the example above, we have equation_numbers np.array([1,2,4,3,5,6]). Note that equation_numbers is 1-indexed In your code snippet, define the function swap_rows_columns, that takes as argument the matrix K and the array equation_numbers and returns the matrix K def swap_rows_columns (K, equation_numbers) # construct the matrix Khat return Khat The setup code provides the matrix K from the example above. You can use it for debugging purposes (since you know what K should look like), but we will test your function using different input arguments. The setup code provides the following variable(s) and/or function(s): Name Type 2d numpy array stiffness matrix corresponding to the example (to help debugging) Description equation_numbers d numpy array ordering of the displacements for partition Your code snippet should define the following variable(s) and/or function(s): Name swap_rows_columns Type unction swaps rows and columns of a matrix Description (1): In typical FEA algorithms, the matrix K is constructed directly, without the need of constructing the matrix K first. user_code.py 1 mport numpy as np 3- def swap_rows_columns(K, equation_numbers)