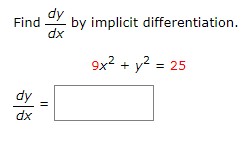
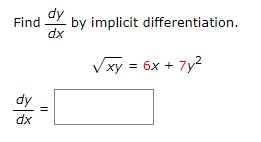
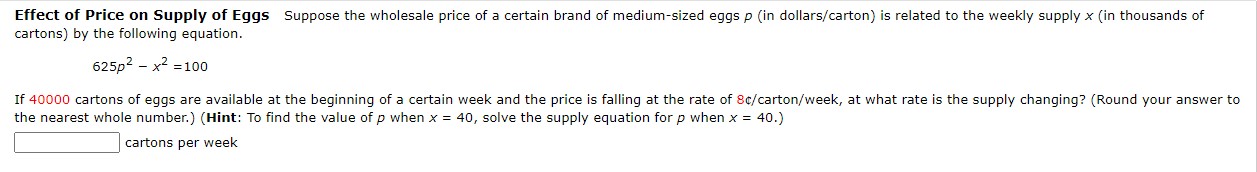
MTH130 Module 2 - Section Assignment 3.6 (Homework)

1.

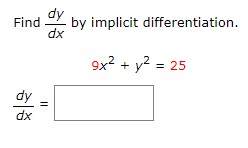
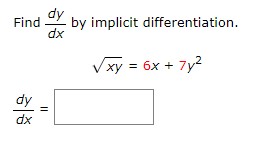
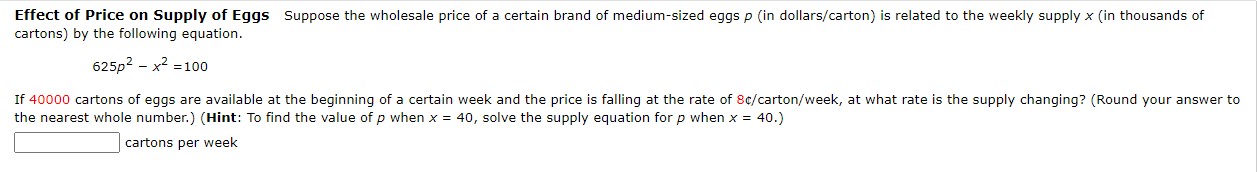
Follow the steps below for the given function. (Do not use mixed numbers in your answers.) 2x + 7y = 7 Solve the equation for y. Differentiate this equation with respect to x. V Complete the steps below to implicitly take the derivative of the original equation. 2x + 7y = 7 dy = 0 dx dy dx dy dxFollow the steps below for the given function. x3 - 7x2 - xy = 1 Solve the equation for y. y Differentiate this equation with respect to x. V' Complete the steps below to implicitly take the derivative of the original equation. (Leave your final answer in terms of x and y.) x5 - 7x2 - xy = 1 -xy = 1 - x3 + 7x2 d -xy) = d (1) d (x 3 ) . d (7x2 ) dx dx dx dx (V) - d (x) = 0 - 3x2 + OX dx dy -X- = -3X2 + y dx dy dxFind BY by implicit differentiation, dx 2 9x + y2 = 25 dy = dxDistance Between Two Cars A car leaves an intersection traveling west. Its position 4 sec later is 21 ft from the intersection. At the same time, another car leaves the same intersection heading north so that its position 4 sec later is 26 ft from the intersection. If the speeds of the cars at that instant of time are 8 ft/sec and 14 ft/sec, respectively, find the rate at which the distance between the two cars is changing. (Round your answer to one decimal place.) ft/sEffect of Price on Supply of Eggs Suppose the wholesale price of a certain brand of medium-sized eggs p (in dollars/carton) is related to the weekly supply x (in thousands of cartons) by the following equation. 625p2 - x2 =100 If 40000 cartons of eggs are available at the beginning of a certain week and the price is falling at the rate of 8c/carton/week, at what rate is the supply changing? (Round your answer to the nearest whole number.) (Hint: To find the value of p when x = 40, solve the supply equation for p when x = 40.) cartons per weekVolume of a Cube The volume V of a cube with sides of length x in. is changing with respect to time. At a certain instant of time, the sides of the cube are 6 in. long and increasing at the rate of 0.3 in./s. How fast is the volume of the cube changing (in cu in/s) at that instant of time? cu in/sWatching a Helicopter Take Off At a distance of 44 ft from the pad, a man observes a helicopter taking off from a heliport. If the helicopter lifts off vertically and is rising at a speed of 51 ft/sec when it is at an altitude of 111 ft, how fast is the distance between the helicopter and the man changing at that instant? ( Round your answer to one decimal place.) ft/secFlow of Water from a Tank Water flows from a tank of constant cross-sectional area 80 ft through an orifice of constant cross-sectional area - ft located at the bottom of the tank. Initially, the height of the water in the tank was 20 ft, and t s later it was given by the equation 2vh + - 1 _t - 2V 20 = 0 0 s t = 80v 20. 40 How fast (in ft/s) was the height of the water decreasing when its height was 9 ft? ft/s