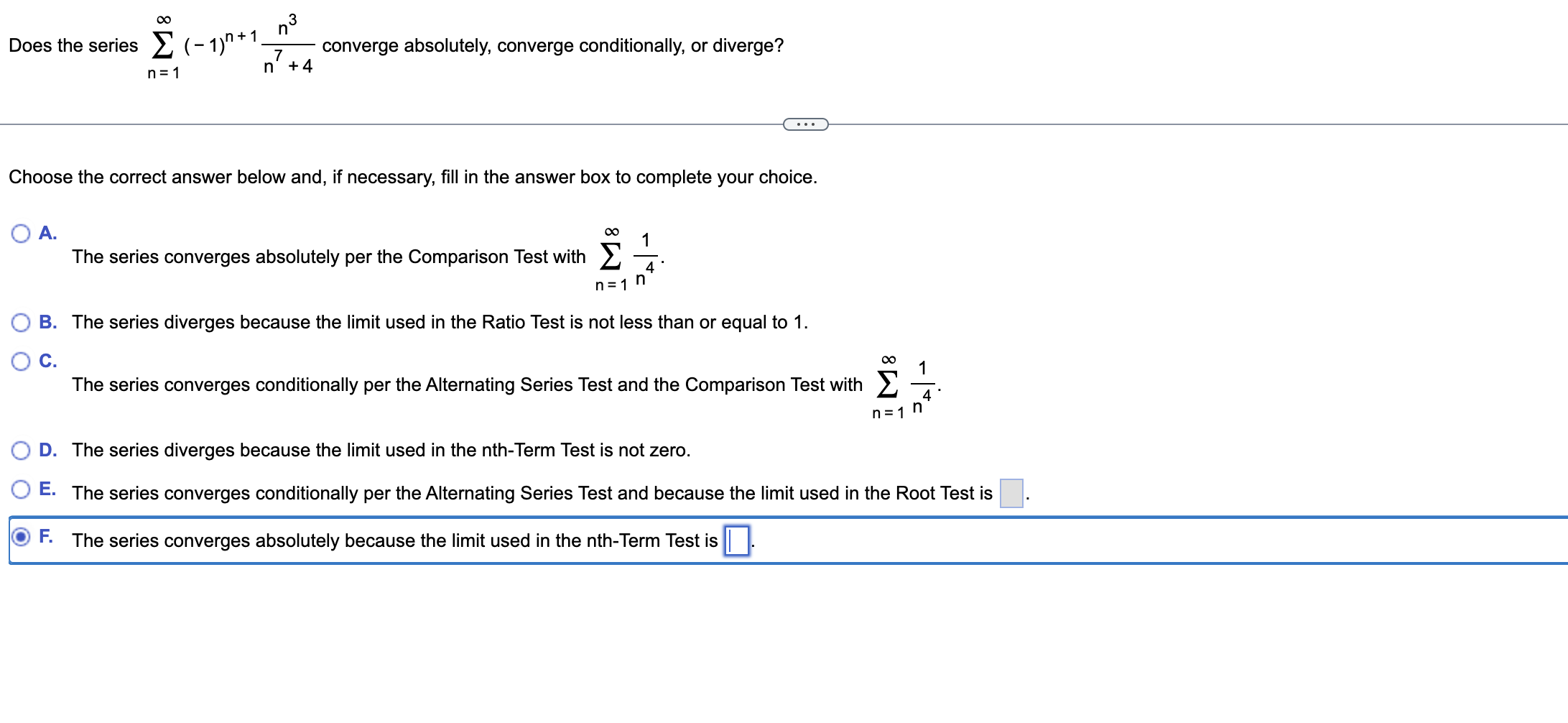
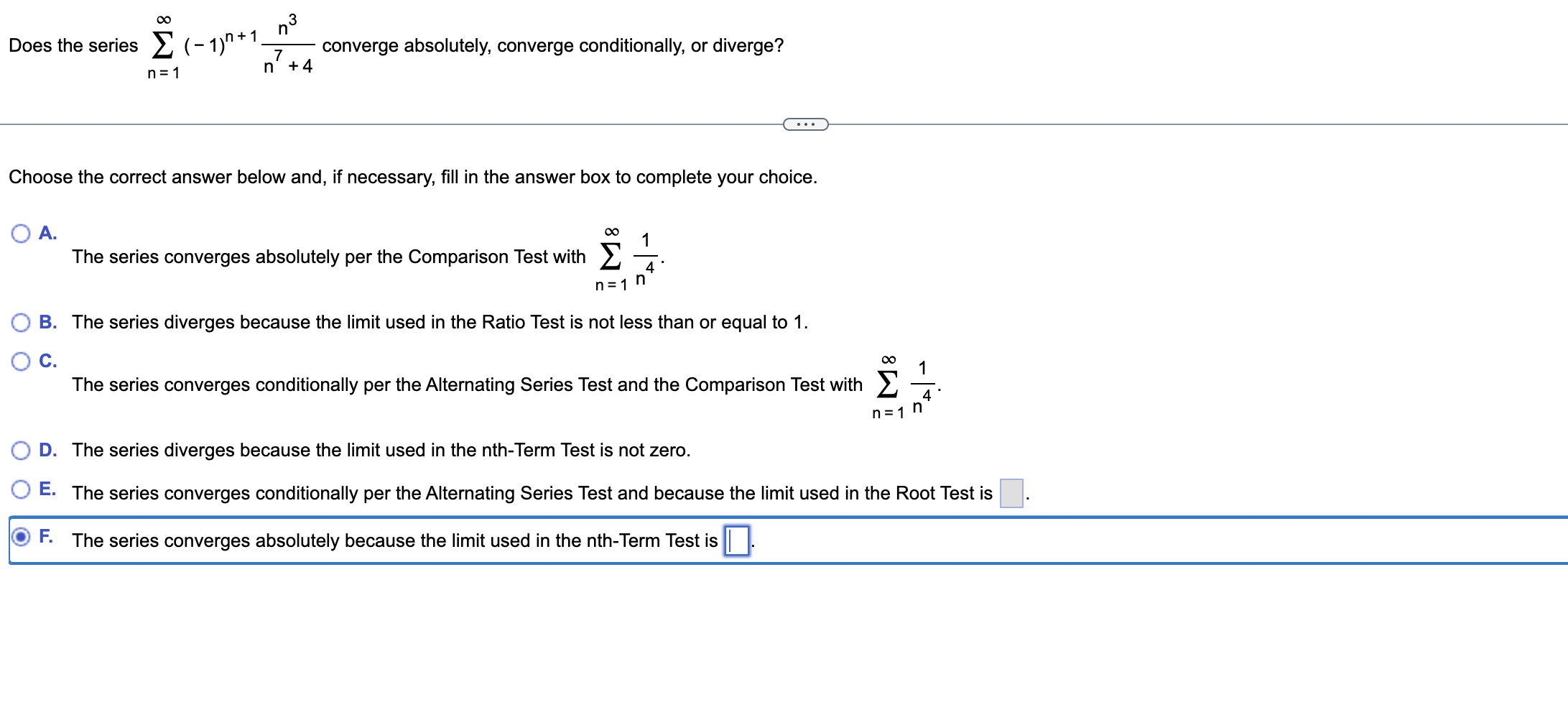
n3 7 n+4 n+1 00 Does the series 2 (- 1) n = 1 converge absolutely, converge conditionally, or diverge? Choose the correct answer below and, if necessary, ll in the answer box to complete your choice. { ':- A. no The series converges absolutely per the Comparison Test with Z 1 4. n=1\" I: ';. B. The series diverges because the limit used in the Ratio Test is not less than or equal to 1. 0C! The series converges conditionally per the Alternating Series Test and the Comparison Test with 2 1 _4_ n=1n I: '2- D. The series diverges because the limit used in the nthTerm Test is not zero. '3._.3' E- The series converges conditionally per the Alternating Series Test and because the limit used in the Root Test is The series converges absolutely because the limit used in the nth-Term Test is ID