Question: Prove by counterexample that the infinite union of compact sets is not necessarily compact. That is, for every natural number k, define a compact

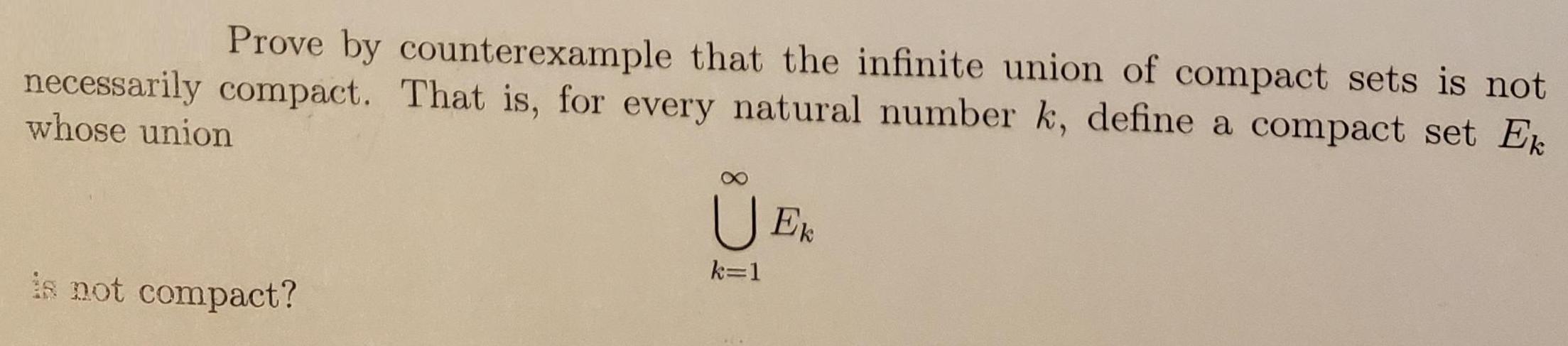
Prove by counterexample that the infinite union of compact sets is not

Prove by counterexample that the infinite union of compact sets is not necessarily compact. That is, for every natural number k, define a compact set Ek whose union is not compact? U EK k=1

Step by Step Solution

★★★★★

3.46 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Suppose by contradiction that the infinite union of compact se... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. The data below shows a group of people plotted by their height and age. Below each person identify their dot on the graph. Please note that the person on the far right is carrying a baby. 2 AGE 7...

Use mathematical induction to prove that, for every natural number n,

Prove that if every even natural number greater than 2 is the sum of two primes, then every odd natural number greater than 5 is the sum of three primes.

Prove De Morgans laws (Theorem 1.4.9). In theorem For every two sets A and B, (A B)c = Ac Bc and (A B)c = Ac Bc.

Use the rules regarding the negation of statements involving quantifiers to write the negation of the following statements. Which is true, the original statement or its negation? (a) Every isosceles...

Find the maximum sum of two positive numbers (not necessarily integers), each of which is in [15 800], and whose product is 800. The maximum sum is E]

(a) Prove that any sequence that converges in the mean square sense must also converge in probability. Use Markovs inequality. (b) Prove by counterexample that convergence in probability does not...

a. Prove, by counter-example, that the statement sec (A + B) sec A + sec B, for all A and B is false. b. Prove that tan + cot 2 cosec 2, n/2, n Z.

(a) Prove that if S, and S, are closed disjoint convex subsets of R", and at least one of them is bounded, then there exists a vector e R" such that sup &'s

Patrick HAYDEN and Melissa Hayden, on behalf of their minor child, A.H., Plaintiffs-Appellants, v. GREENSBURG COMMUNITY SCHOOL CORPORATION, et al., Defendants-Appellees. No. 13-1757.Decided: February...

Data mining is the process of using sophisticated statistical techniques to extract and analyze data from large databases to discern patterns and trends that were not previously known. The patterns...

You are the new accounting intern. You have been charged with improving risk intelligence related to the organizations 1,000 spreadsheets. You have been asked to make a presentation to the CFO and...

Two spaceships are moving directly toward one another ith a relative velocity of 0.90c. If an astronaut measures the length of his own spaceship to be 30.0 m, how long is the spaceship as measured by...

a Expand (1 + x) ^ 5 b Use your answer to part a to express i (1 + sqrt(3)) ^ 5 in the form a + b * sqrt(3) ii (1 - sqrt(3)) ^ 5 in the form c + d * sqrt(3) c Use your answers to part b to simplify...

Identify the given stakeholders or viewpoints in the context of listed software systems. System Medical Information System Autoteller System (ATM) Hotel Management System Online Ticket Reservation...

Manny was arrested as the main suspect in a murder investigation. Manny was brought into an interrogation room, but was not read his Miranda rights. A police officer asked Manny, Where were you on...

Q.8) (7 Marks) The linear mass density of a thin rod is given by p = cx2, where c is a constant and x is the distance measured from the origin. If the rod is of length b, find (a) the center of mass...

Q.7) (6 Marks) A system consists of two particles, each of mass m=5 g, with positions and velocities as follows: ri = (2 + 2) ) cm V1 = 4 cm/s r = (4)+ 4k) cm V2 = 2j cm/s Find (a) the linear...

What is the role of the acceptor arm of the NA me? binding to the codon sequence of the MRNA binding a specific amino acid binding to the ribosome binding to the growing polypeptide chain Question 10...

Problem1 A Bit Vector Framework is a special instance of a monotone framework where L = (P(D), ) for some finite set D and where P(D) is the powerset of D and is either set union (U) or set...

(4 marks: 2 marks for counterexample, 2 marks for question on closure under complement) Prove by counterexample that if M is a NFA that recognizes languages B, then swapping the accept and nonaccept...

3. Algorithm Correctness (10 points) A different modification of NAVE-STRING-MATCHER the effectively implements the same strategy is given below. But it is an incorrect algorithms....

This question illustrates differences and commonalities between NFAs and DFAs. (a) Show that if M is a DFA that recognizes language B, then swapping the accept and nonaccept states in M yields a new...

theory of computation 1) Show that if M is a DFA that recognizes language B, then swapping the accept and nonaccept states in M yields a new DFA M0 recognizing the complement of B, B. Which operation...

The last three picture Consider a two-person household. These two people have very similar preferences (that's why they enjoy living together), which are described by the following utility...