(need answers for this question)

the transportation problem

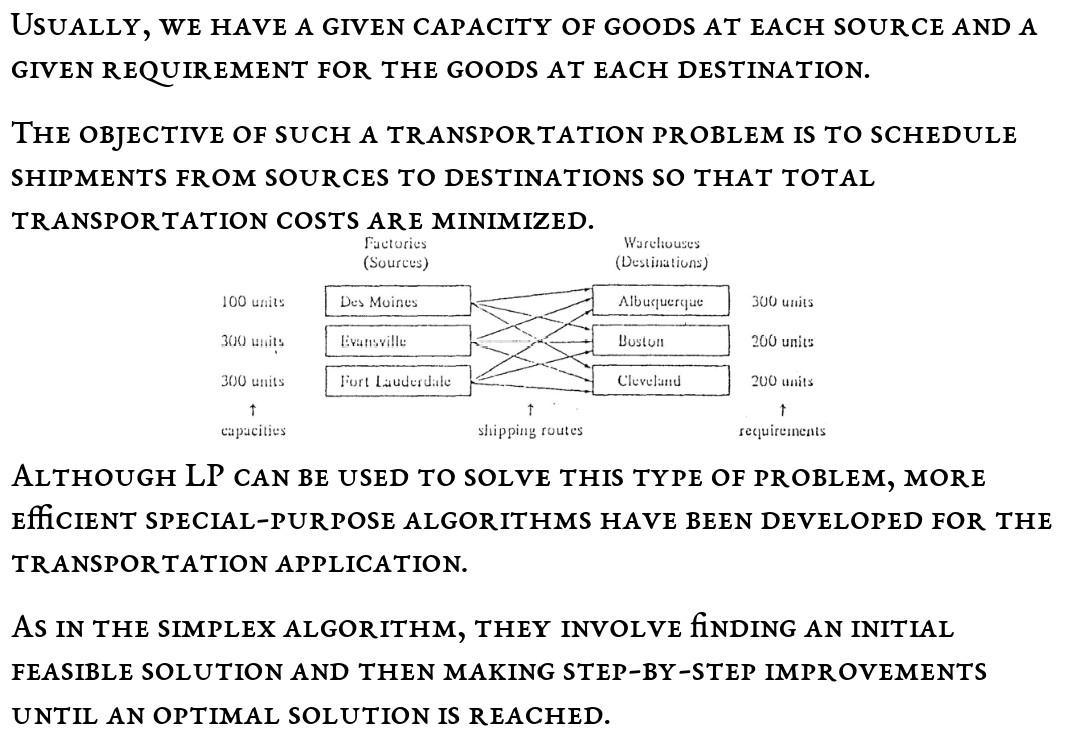
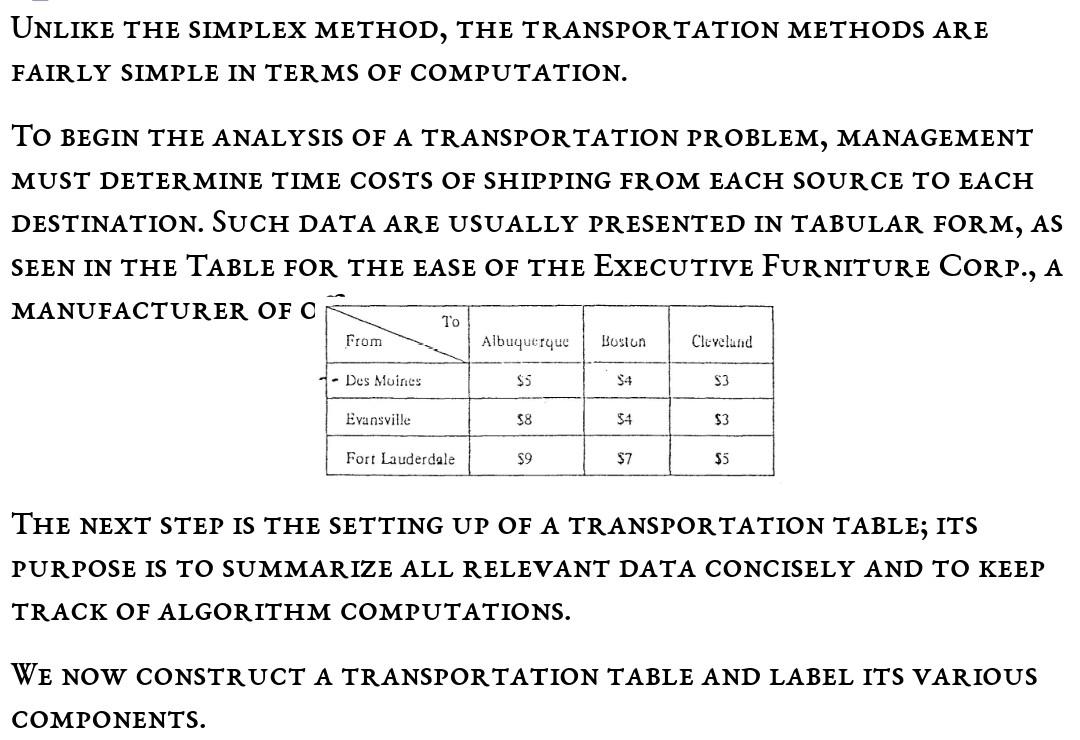
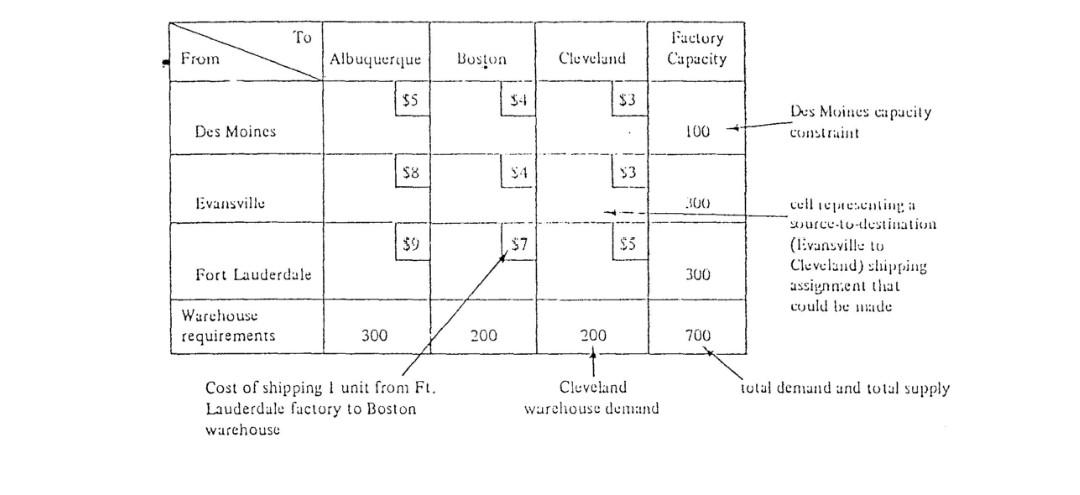
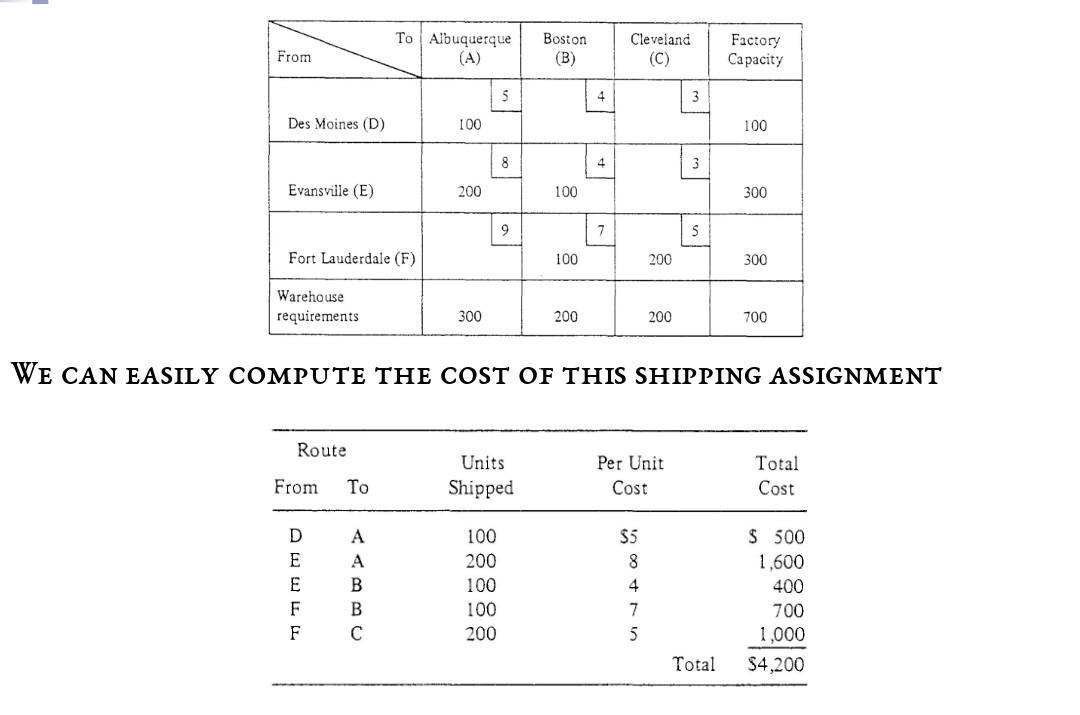
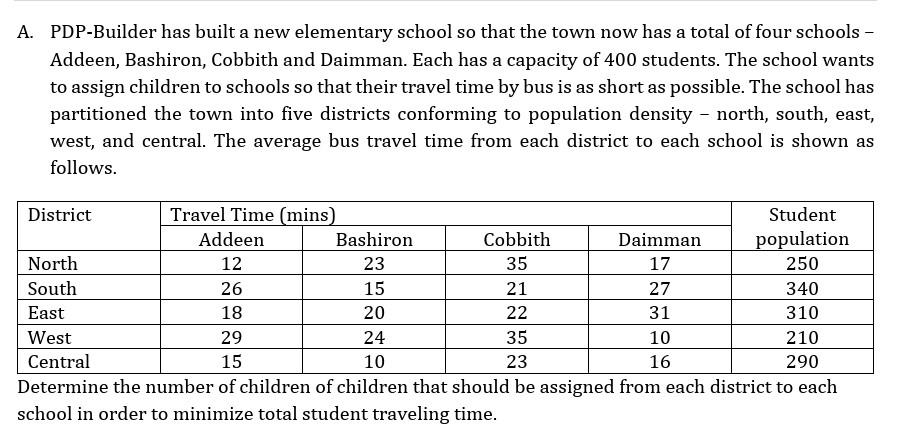
A. PDP-Builder has built a new elementary school so that the town now has a total of four schools - Addeen, Bashiron, Cobbith and Daimman. Each has a capacity of 400 students. The school wants to assign children to schools so that their travel time by bus is as short as possible. The school has partitioned the town into five districts conforming to population density - north, south, east, west, and central. The average bus travel time from each district to each school is shown as follows. District Travel Time (mins) Student Addeen Bashiron Cobbith Daimman population North 12 23 35 17 250 South 26 15 21 27 340 East 18 20 22 31 310 West 29 35 210 Central 15 10 23 16 290 Determine the number of children of children that should be assigned from each district to each school in order to minimize total student traveling time. 24 10 USUALLY, WE HAVE A GIVEN CAPACITY OF GOODS AT EACH SOURCE AND A GIVEN REQUIREMENT FOR THE GOODS AT EACH DESTINATION. THE OBJECTIVE OF SUCH A TRANSPORTATION PROBLEM IS TO SCHEDULE SHIPMENTS FROM SOURCES TO DESTINATIONS SO THAT TOTAL TRANSPORTATION COSTS ARE MINIMIZED. Factories (Sources) Warehouses (Destinations) 100 units Des Moines Albuquerque 300 units 300 unit livansville Boston 200 units 300 units Fort Lauderdale Cleveland 200 units 1 capacities 1 Shipping routes 1 requirements ALTHOUGH LP CAN BE USED TO SOLVE THIS TYPE OF PROBLEM, MORE EffiCIENT SPECIAL-PURPOSE ALGORITHMS HAVE BEEN DEVELOPED FOR THE TRANSPORTATION APPLICATION. AS IN THE SIMPLEX ALGORITHM, THEY INVOLVE FINDING AN INITIAL FEASIBLE SOLUTION AND THEN MAKING STEP-BY-STEP IMPROVEMENTS UNTIL AN OPTIMAL SOLUTION IS REACHED. UNLIKE THE SIMPLEX METHOD, THE TRANSPORTATION METHODS ARE FAIRLY SIMPLE IN TERMS OF COMPUTATION. TO BEGIN THE ANALYSIS OF A TRANSPORTATION PROBLEM, MANAGEMENT MUST DETERMINE TIME COSTS OF SHIPPING FROM EACH SOURCE TO EACH DESTINATION. SUCH DATA ARE USUALLY PRESENTED IN TABULAR FORM, AS SEEN IN THE TABLE FOR THE EASE OF THE EXECUTIVE FURNITURE CORP., A MANUFACTURER OF O Albuquerque To From Boston Cleveland Des Moines $5 S3 Evansville $8 $4 $3 Fort Lauderdale $9 S7 S5 THE NEXT STEP IS THE SETTING UP OF A TRANSPORTATION TABLE; ITS PURPOSE IS TO SUMMARIZE ALL RELEVANT DATA CONCISELY AND TO KEEP TRACK OF ALGORITHM COMPUTATIONS. WE NOW CONSTRUCT A TRANSPORTATION TABLE AND LABEL ITS VARIOUS COMPONENTS. Factory Capacity From Albuquerque Boston Cleveland $5 54 Des Moines capacity Construint Des Moines 100 $8 3 Evansville 300 $7 $3 cell presenting a urce-to-testination (livansville to Cleveland) shipping assiynn.ent that could be made Fort Lauderdale 300 Warehouse requirements 300 200 200 700 Cost of shipping I unit from Ft. Lauderdale factory to Boston warehouse Cleveland warehouse demand total demand and total supply DEVELOPING AN INITIAL SOLUTION THE NORTHWEST CORNER RULE ONCE THE DATA HAVE BEEN ARRANGED IN TABULAR FORM, WE MUST ESTABLISH AN INITIAL FEASIBLE SOLUTION TO THE PROBLEM (JUST AS WE DID IN THE FIRST LP SIMPLEX TABLE). ONE SYSTEMATIC PROCEDURE, KNOWN AS THE NORTHWEST CORNER RULE, REQUIRES THAT WE START IN THE UPPER LEFT HAND CELL (OR NORTHWEST CORNER) OF THE TABLE AND ALLOCATE UNITS TO SHIPPING ROUTES AS FOLLOWS: EXHAUST THE SUPPLY (FACTORY SUPPLY) AT EACH ROW BEFORE MOVING DOWN TO THE NEXT ROW. EXHAUST THE (WAREHOUSE) REQUIREMENTS OF EACH COLUMN BEFORE MOVING TO THE NEXT COLUMN, ON THE RIGHT. CHECK THAT ALL THE SUPPLY AND DEMANDS ARE MET. EXAMPLE 13.1 WE CAN USE THE NORTHWEST CORNER RULE TO FIND AN INITIAL FEASIBLE SOLUTION TO THE EXECUTIVE FURNITURE CORP. PROBLEM SHOWN IN THE TABLE. IT TAKES FIVE STEPS IN THIS EXAMPLE TO MAKE THE INITIAL SHOPPING ASSIGNMENTS: ASSIGN 100 UNITS FROM DES MOINES TO ALBUQUERQUE (EXHAUSTING DES MOINES SUPPLY). ASSIGN 200 UNITS FROM EVANSVILLE TO ALBUQUERQUE (EXHAUSTING ALBUQUERQUE'S DEMAND). ASSIGN 100 UNITS FROM EVANSVILLE TO BOSTON (EXHAUSTING EVANSVILLE'S SUPPLY). ASSIGN 100 UNITS FROM FT. LAUDERDALE TO BOSTON (EXHAUSTING BOSTON'S DEMAND). ASSIGN 200 UNITS FROM FT. LAUDERDALE TO CLEVELAND (EXHAUSTING CLEVELAND'S DEMAND AND FT. LAUDERDALES SUPPLY). To Albuquerque (A) From Boston (B) Cleveland (C) Factory Capacity 5 4 3 Des Moines (D) 100 100 8 4 3 Evansville (E) 200 100 300 9 7 S Fort Lauderdale (F) 100 200 300 Warehouse requirements 300 200 200 700 WE CAN EASILY COMPUTE THE COST OF THIS SHIPPING ASSIGNMENT Route Units Shipped Per Unit Cost Total Cost From A S5 8 D E E F F B 100 200 100 100 200 4 S 500 1,600 400 700 1,000 $4,200 B 7 5 Total THE SOLUTION GIVEN HERE IS FEASIBLE SINCE DEMAND-AND-SUPPLY CONSTRAINTS ARE ALL SATISFIED. IT WOULD BE VERY LUCKY IF THIS SOLUTION YIELDED THE MINIMAL TRANSPORTATION COST FOR THE PROBLEM, HOWEVER. IT IS MORE LIKELY THAT ONE OF THE ITERATIVE PROCEDURES DESIGNED TO HELP REACH AN OPTIMAL SOLUTION SHALL HAVE TO BE EMPLOYED. FIRST, TRY TO USE THE METHOD TO SOLVE PROBLEM 13.I