Need asap :)

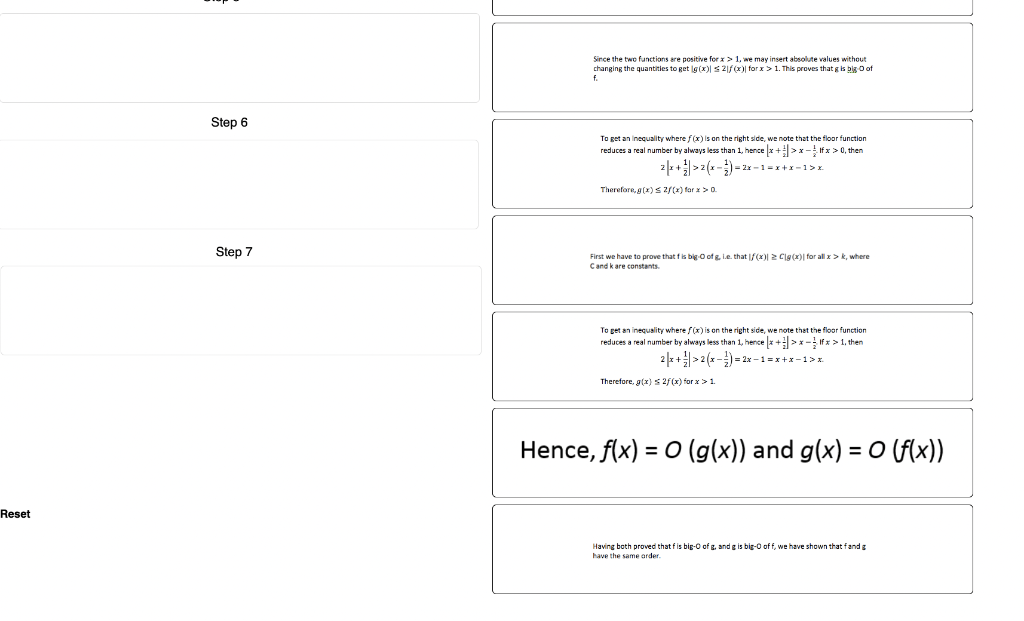
Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Click and drag the steps to their corresponding step numbers to prove that the given pair of functions are of the same order. (Note: Consider to prove the result, first prove f(x)=O(g(x)) and then prove g(x)=O(f(x)). f(x)=x+21andg(x)=x f(x)=x+21andg(x)=x. Secondly; we have to prove that g is big-0 of f1 i.e, that lg(x)Cf(x) for sll x>k, where C and k are constants. Step 1 Forx>2,[x+21]2x Secondly, we have to prove that g is big-0 of f, i.e. that g(x)cf(x) for al| x>k, ahere C and k are constants. Step 3 For x>2,x2x+21 Dbserve that for all x>k=0,x+x1k, or f() 2g(x) Step 5 Sirce the two functians are pesitive for x>1, we may insert absolute values without changing the quantities to get g(x)2f(x) for x>1. This proves that g b bigo of Step 6 To get an inequality where f(x) is on the right side, we note that the floar function reduces a real number by always less than 1 , hence x+21>x21 If x>0, then reduces a real number by always less than 1 , hence [x+21>x21 - If x>1. 2x+21>2(x21)=2x1=x+x1>x Step 7 First we have to prove Cand k are constants. To cet an inequality where f(x) is on the right side, we note that the floor function reduces a real number by always less than 1 , hence x+21>x21 If x>1, then 2x+21>2(x21)=2x1=x+x1>x Therefore, g(x)2f(x) for x>1 Hence, f(x)=O(g(x)) and g(x)=O(f(x)) Reset