Need help!!

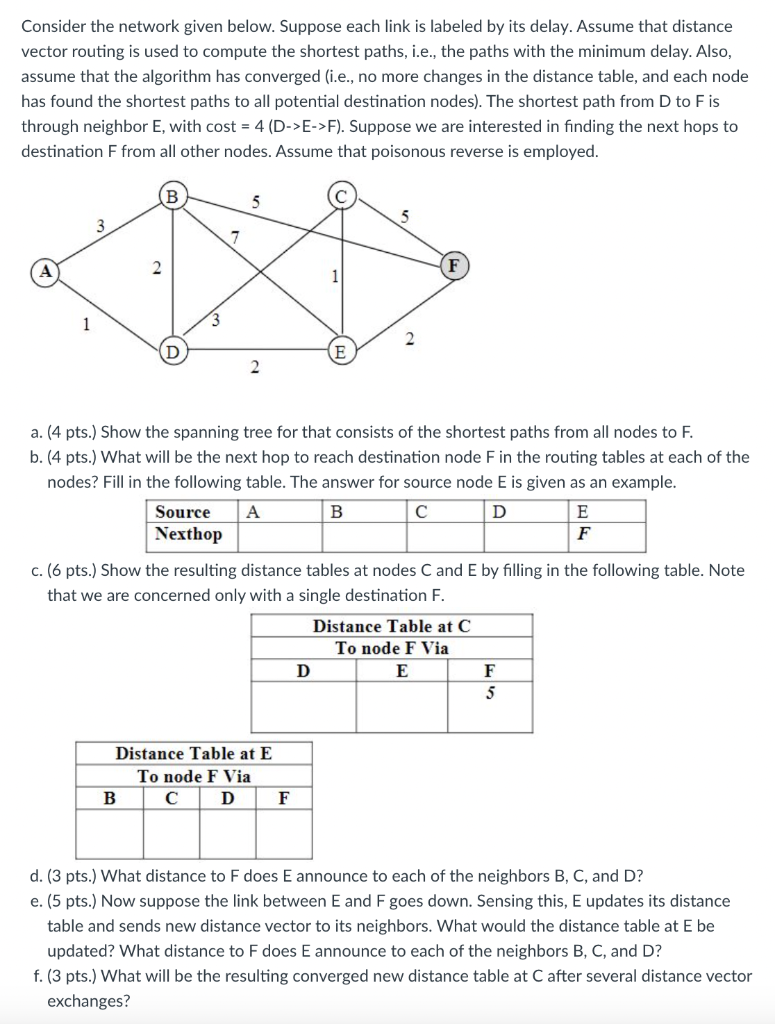
Consider the network given below. Suppose each link is labeled by its delay. Assume that distance vector routing is used to compute the shortest paths, i.e., the paths with the minimum delay. Also, assume that the algorithm has converged (i.e., no more changes in the distance table, and each node has found the shortest paths to all potential destination nodes). The shortest path from D to F is through neighbor E, with cost = 4 (D->E->F). Suppose we are interested in finding the next hops to destination F from all other nodes. Assume that poisonous reverse is employed. a. (4 pts.) Show the spanning tree for that consists of the shortest paths from all nodes to F. b. (4 pts.) What will be the next hop to reach destination node F in the routing tables at each of the nodes? Fill in the following table. The answer for source node E is given as an example. c. (6 pts.) Show the resulting distance tables at nodes C and E by filling in the following table. Note that we are concerned only with a single destination F. d. (3 pts.) What distance to F does E announce to each of the neighbors B,C, and D ? e. (5 pts.) Now suppose the link between E and F goes down. Sensing this, E updates its distance table and sends new distance vector to its neighbors. What would the distance table at E be updated? What distance to F does E announce to each of the neighbors B,C, and D ? f. ( 3 pts.) What will be the resulting converged new distance table at C after several distance vector exchanges