Need help with my last couple Computer Science questions regarding Dynamic Programming

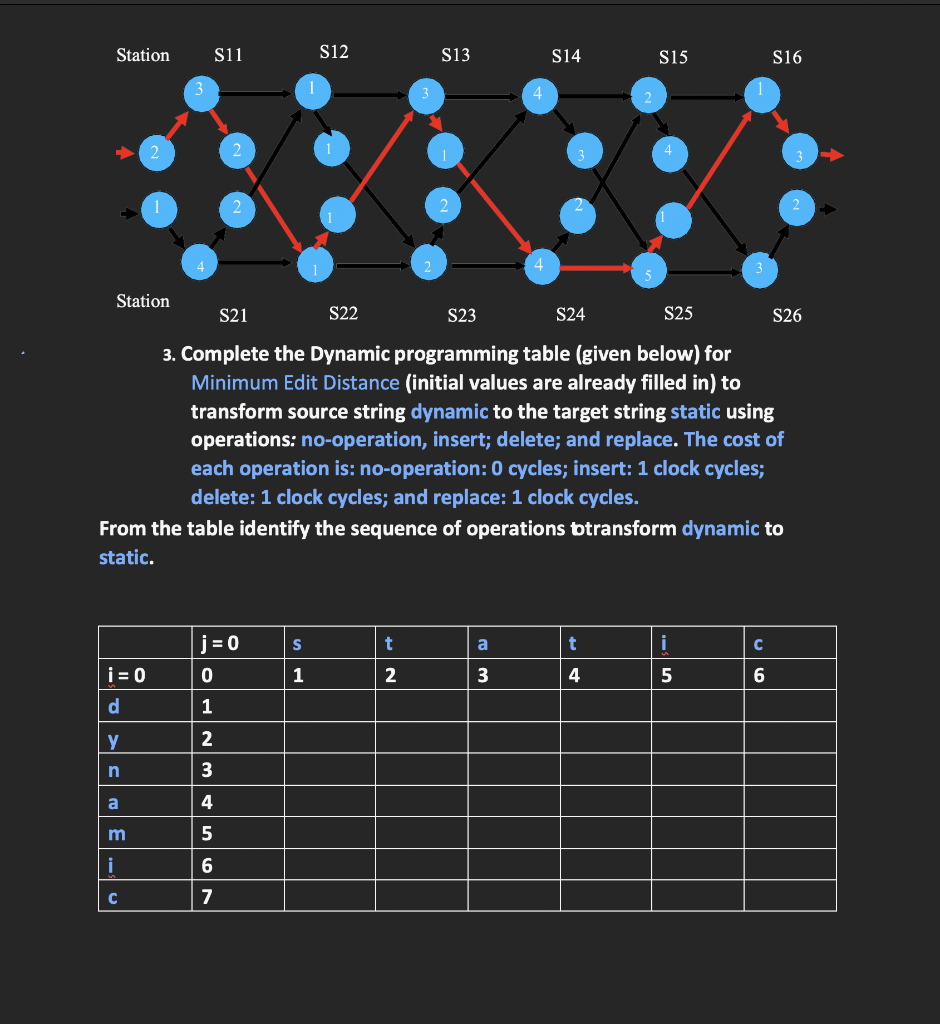
1. Complete the following table constructed by the Dynamic Programming (DP) algorithm for finding the Longest Common Sub-Sequence (LCS) between two sequences X and Y. Also highlight the characters in the LCS table. X=(A,B,C,B,D,A,B)andY=(B,D,C,A,B,A) 2. for the following instance of the Assembly-Line Scheduling problem, complete the following table constructed by the Dynamic Programming (DP) algorithm. The station time and the transfer times are indicated in the diagram below. 3. Complete the Dynamic programming table (given below) for Minimum Edit Distance (initial values are already filled in) to transform source string dynamic to the target string static using operations: no-operation, insert; delete; and replace. The cost of each operation is: no-operation: 0 cycles; insert: 1 clock cycles; delete: 1 clock cycles; and replace: 1 clock cycles. From the table identify the sequence of operations btransform dynamic to static. 4. A sequence of numbers x, which includes both positive and negative numbers, is given below. Use the Algorithm, which is based on Design-by-Induction, to determine the Maximum Consecutive Subsequence (MCS). Complete the table, filling in the values of Global Max and Suffix Max as the algorithm proceeds for values of i from 1 to 12 . The table is provided for your convenience. Highlight the Consecutive Subsequence with Maximum sum