Question: need help with this 17. Show that every Cauchy sequence is bounded. (Hint use GNU instead of a in the above exercise) 18. Show that

need help with this

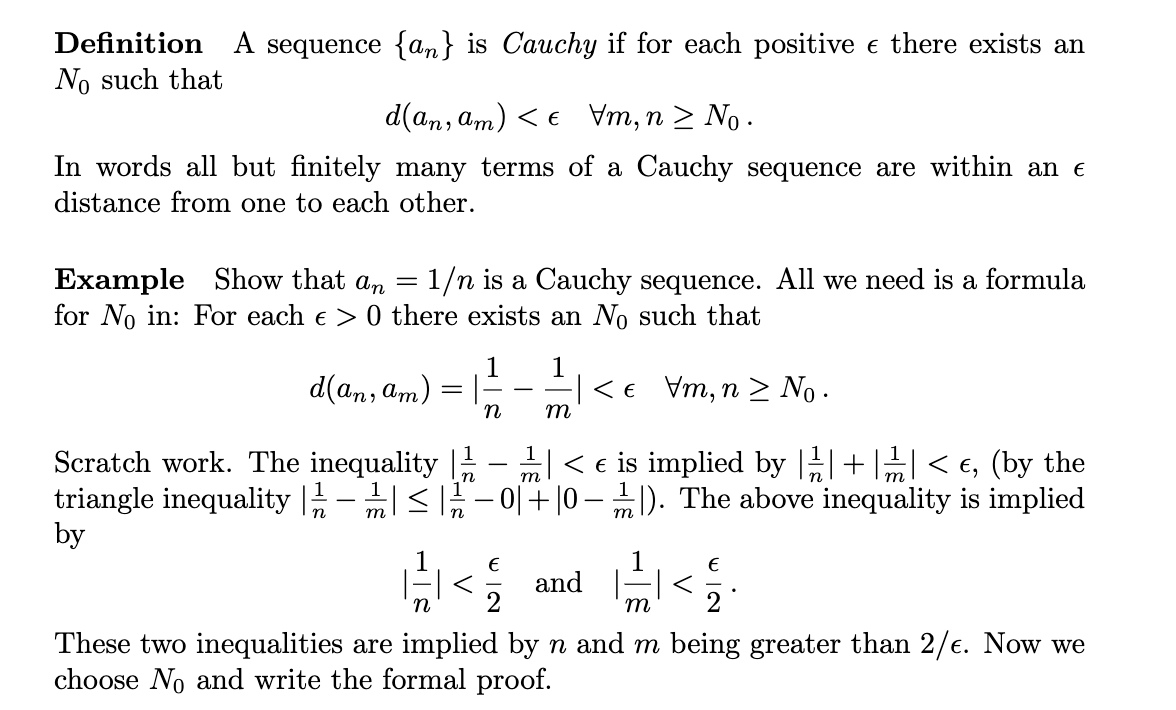
17. Show that every Cauchy sequence is bounded. (Hint use GNU instead of a in the above exercise) 18. Show that every convergent sequence is a Cauchy sequence. Definition A sequence {an} is Cauchy if for each positive e there exists an No such that d(an, am) No. In words all but finitely many terms of a Cauchy sequence are within an e distance from one to each other. Example Show that an = 1 is a Cauchy sequence. All we need is a formula for No in: For each e > 0 there exists an No such that d(an, am) = | n m No. Scratch work. The inequality |2 - - |

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

# 7 (chapter 5)(40 points, Due on Friday November 11) Question 1. [3 points each] Use the definition of Limit of functions to prove that x2 2 . 5 5 2 lim x 3 x 1 1 (B) x 1 (A) lim x 0 if x 2 2x (C)...

1. Suppose we have a sequence {xk} with x1 x2 x3 x4 and we also have an upper bound M with xk M for all xk. Prove that this sequence must have a limit. Hint: you must use the completeness...

You$must$attach$this$cover$page$to$the$front$of$your$HW$or$you$will$lose$5$points.$ $ $ APMA$1860$Homework$2$ $ $ First$Name:$____________________________$$$Last$Name:$______________________________$...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

True False or Incoherent 1. A countable union of countable sets is countable. 2. An arbitrary union of countable sets is countable. 3. A finite Cartesian product of countable sets is always...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Computer Organization and Networks Practicals 2021/22 October 9, 2021 Computer Organization and Networks Practicals 2021/22 b68495714b Contents Contents 0 Introduction 3 0.1 Registration . . . . . ....

Let $\left(e_{n}ight)_{n \in \mathbb{N}} \subset \mathcal{H}$ be an orthonormal system. (i) Show that no subsequence of $\left(e_{n}ight)_{n \in \mathbb{N}}$ converges. However, for every \(h \in...

State whether each of the following is or is not a principle (or a portion of a principle) underlying an audit conducted in accordance with Generally Accepted Auditing Standards. Principles Yes (Y)...

How does the human resources cycle and payroll affect the cost accounting records?

Find the future value of the annuity. Round your answer to the nearest cent. \ table [ [ Payment , Rate,Compounded,Time ] , [ $ 3 1 0 0 , 1 . 7 3 % , Quarterly, 6 1 2 years ] ] The future value of...

A company issues 1,050 shares of its common stock for $33,600 cash. Prepare journal entries to record this event under each of the following separate situations.