Need some help please

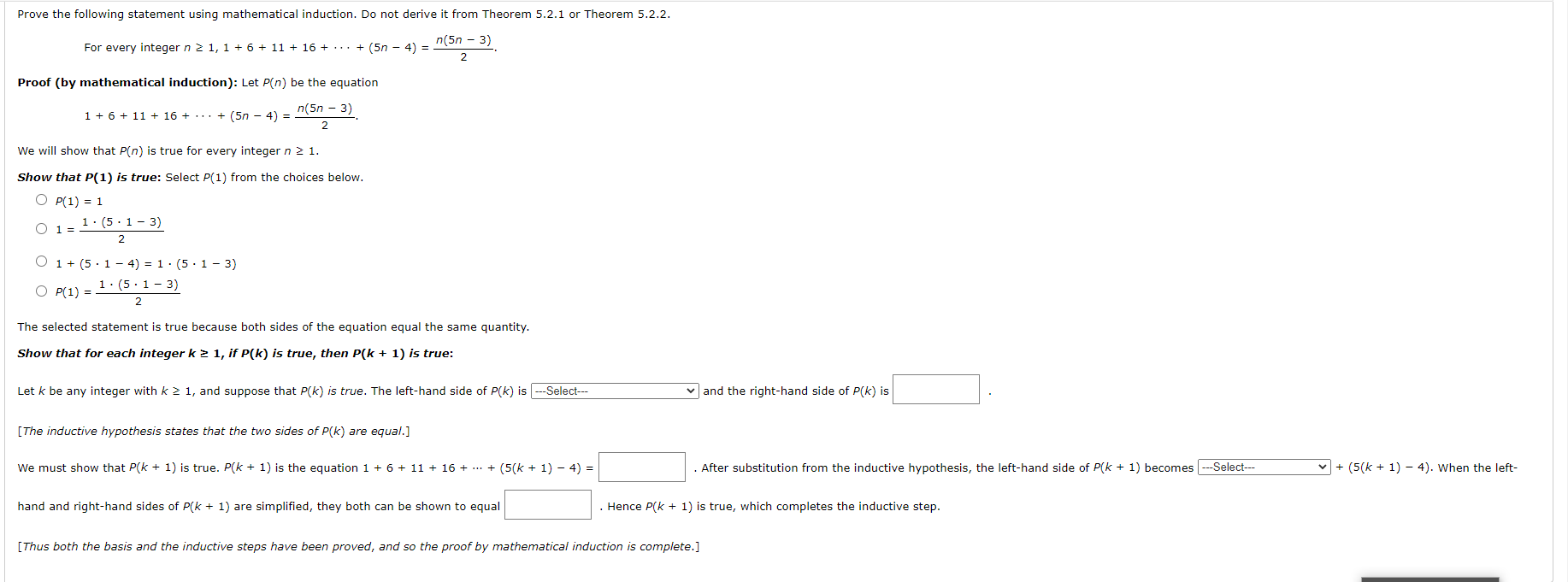
Prove the following statement using mathematical induction. Do not derive it from Theorem 5.2.1 or Theorem 5.2.2. For every integer n 2 1, 1 + 6 + 11 + 16 + . . . + (5n - 4) = n(5n - 3) 2 Proof (by mathematical induction): Let P(n) be the equation 1 + 6 + 11 + 16 + . . . + (50 - 4) = n(5n - 3) 2 We will show that P(n) is true for every integer n 2 1. Show that P(1) is true: Select P(1) from the choices below. O P(1) = 1 O 1= 1. (5 . 1 -3) O 1 + (5 . 1 - 4) = 1 . (5 . 1 - 3) O P(1) = 1 . (5 . 1 - 3) The selected statement is true because both sides of the equation equal the same quantity. Show that for each integer k 2 1, if P(k) is true, then P(k + 1) is true: Let k be any integer with k 2 1, and suppose that P(k) is true. The left-hand side of P(k) is ---Select--- | and the right-hand side of P(k) is [ The inductive hypothesis states that the two sides of P(k) are equal.] We must show that P(k + 1) is true. P(k + 1) is the equation 1 + 6 + 11 + 16 + ... + (5(k + 1) - 4) = . After substitution from the inductive hypothesis, the left-hand side of P(k + 1) becomes ---Select--- v + (5(k + 1) - 4). When the left- hand and right-hand sides of P(k + 1) are simplified, they both can be shown to equal Hence P(k + 1) is true, which completes the inductive step. [Thus both the basis and the inductive steps have been proved, and so the proof by mathematical induction is complete.]