Question: need state and steps Let a and b be positive integers. Prove that if ma2 + nb2 = god(a, b) for some integers m and

need state and steps

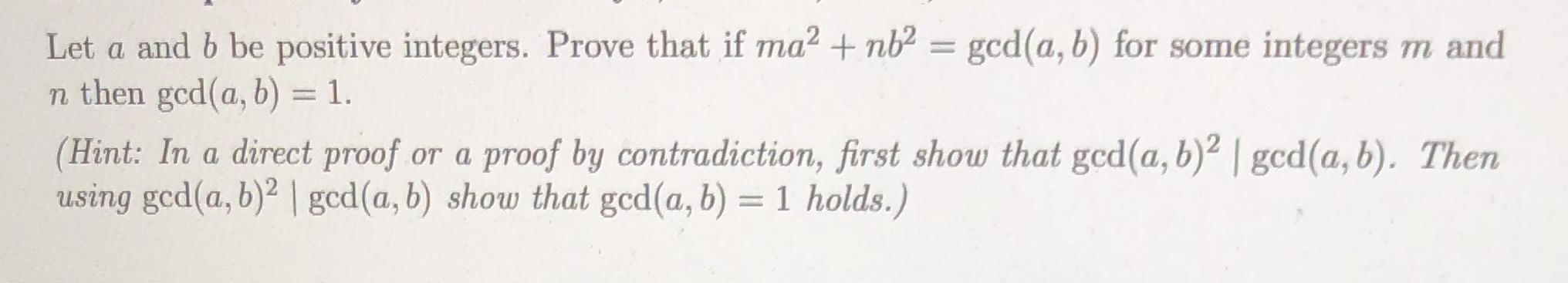
Let a and b be positive integers. Prove that if ma2 + nb2 = god(a, b) for some integers m and n then god(a, b) = 1. (Hint: In a direct proof or a proof by contradiction, first show that god(a, b)2 | god(a, b). Then using god(a, b)2 | god(a, b) show that god(a, b) = 1 holds.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

6. Calculate the following problems (18 pts). a. 7+1334= b. 51119= c. 17+131= d. 47+130= e. 55111= f. 55110=0 7. Express gcd(990,502)=2 as a linear combination of 990 and 502 by working backwards...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

4. Let d be a positive integer that is greater than or equal to 2. (a) Let x and y be nonzero integers. Prove that if yd | ad and god(x, y) = 1 then y = 11. (b) Let a be a positive integer. Prove...

Lecture: Overview - Introduction 1 . a , b in N ( positive integers ) , prove that: a mod b = b mod a iff a = b ( 2 0 points ) Lecture: Overview - Introduction 2 . Prove or disapprove that: If a , b...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

On June 3, Donald and Sonna Hummel executed a written purchase order invoice for the purchase of a 1989 Chevrolet Corsica from Raisor Pontiac in Lafayette, Indiana. The purchase order indicated that...

Harry Gultekin, a small restaurant owner/manager, is contemplating the purchase of a larger restaurant from its owner who is retiring. Gultekin would finance the purchase by selling his existing...

Carlton Company uses the percent of sales method to estimate its bad debt expense Based on past experience the company estimates 2 percent of credit sales to be uncollectible At the end of the...

A company issues 1,050 shares of its common stock for $33,600 cash. Prepare journal entries to record this event under each of the following separate situations.