need the ans now

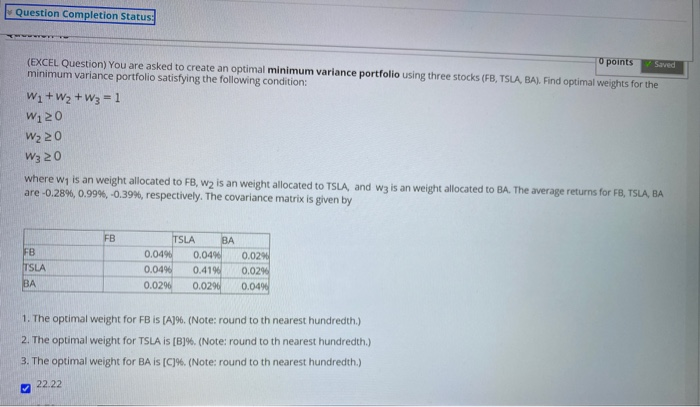
Question Completion Status O points Saved (EXCEL Question) You are asked to create an optimal minimum variance portfolio using three stocks (FB, TSLA, BA). Find optimal weights for the minimum variance portfolio satisfying the following condition: Wa+W2+W3 = 1 W120 W220 W320 where w is an weight allocated to FB, W2 is an weight allocated to TSLA, and w3 is an weight allocated to BA. The average returns for FB, TSLA, BA are -0.28%, 0.99%, -0.39%, respectively. The covariance matrix is given by FB FB TSLA BA TSLA BA 0.0490 0.0490 0.04 0.4196 0.0296 0.02% 0.02% 0.02% 0.049 1. The optimal weight for FB is [A]%. (Note: round to th nearest hundredth.) 2. The optimal weight for TSLA IS [B]%. (Note: round to th nearest hundredth.) 3. The optimal weight for BA is (C)%. (Note: round to th nearest hundredth.) 22.22 Question Completion Status O points Saved (EXCEL Question) You are asked to create an optimal minimum variance portfolio using three stocks (FB, TSLA, BA). Find optimal weights for the minimum variance portfolio satisfying the following condition: Wa+W2+W3 = 1 W120 W220 W320 where w is an weight allocated to FB, W2 is an weight allocated to TSLA, and w3 is an weight allocated to BA. The average returns for FB, TSLA, BA are -0.28%, 0.99%, -0.39%, respectively. The covariance matrix is given by FB FB TSLA BA TSLA BA 0.0490 0.0490 0.04 0.4196 0.0296 0.02% 0.02% 0.02% 0.049 1. The optimal weight for FB is [A]%. (Note: round to th nearest hundredth.) 2. The optimal weight for TSLA IS [B]%. (Note: round to th nearest hundredth.) 3. The optimal weight for BA is (C)%. (Note: round to th nearest hundredth.) 22.22