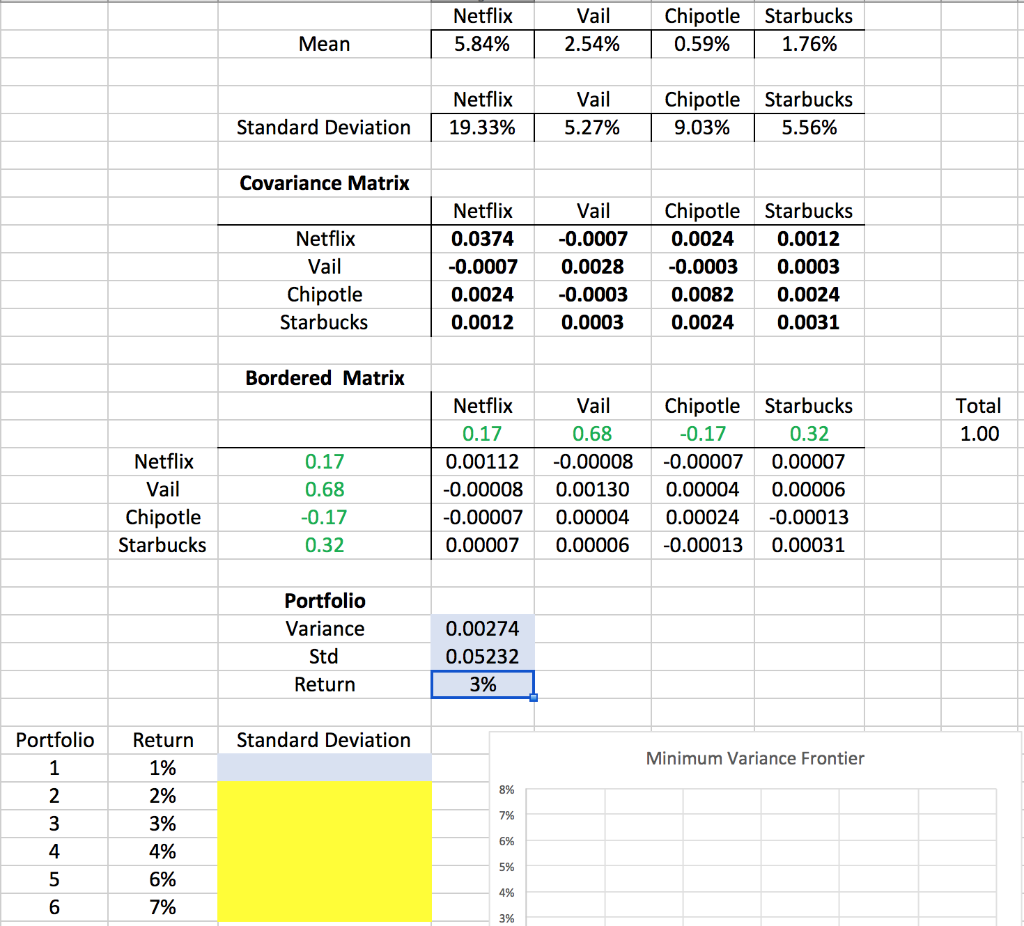
Netflix 5.84% Vail 2.54% Chipotle Starbucks 0.59% 1.76% Mean Netflix 19.33% Vail 5.27% Chipotle Starbucks 9.03% 5.56% Standard Deviation Covariance Matrix Netflix Vail Chipotle Starbucks Netflix 0.0374 -0.0007 0.0024 0.0012 Vail -0.0007 0.0028 -0.0003 0.0003 Chipotle Starbucks 0.0024 0.0012 -0.0003 0.0003 0.0082 0.0024 0.0024 0.0031 Bordered Matrix Total 1.00 Netflix Vail Chipotle Starbucks 0.17 0.68 -0.17 0.32 Netflix 0.17 0.00112 -0.00008 -0.00007 0.00007 Vail 0.68 -0.00008 0.00130 0.00004 0.00006 Chipotle Starbucks -0.17 0.32 -0.00007 0.00007 0.00004 0.00006 0.00024 -0.00013 -0.00013 0.00031 Portfolio Variance Std Return 0.00274 0.05232 3% Standard Deviation Minimum Variance Frontier Portfolio 1 2 8% 7% Return 1% 2% 3% 4% 6% 7% 3 4 5 6 6% 5% 4% 3% 3. Calculate the minimum variance frontier for return increments 1%-7%. Report the variance of each. (hint: when you calculated the minimum variance you did so unconstrained. Now you will need to constrain returns to be a certain value) 4. Calculate the optimal portfolio for an investor with risk aversion parameter A=4 and A=64. Report the utility of each. 5. Now add a new asset called Rifi that offers 0% return and has 0% standard deviation of returns and is uncorrelated with other assets. (what should the covariance matrix row/column look like for this new asset). For the A=64 investor, what is the new optimal risk and return if they can include Rifi as part of their portfolio? Netflix 5.84% Vail 2.54% Chipotle Starbucks 0.59% 1.76% Mean Netflix 19.33% Vail 5.27% Chipotle Starbucks 9.03% 5.56% Standard Deviation Covariance Matrix Netflix Vail Chipotle Starbucks Netflix 0.0374 -0.0007 0.0024 0.0012 Vail -0.0007 0.0028 -0.0003 0.0003 Chipotle Starbucks 0.0024 0.0012 -0.0003 0.0003 0.0082 0.0024 0.0024 0.0031 Bordered Matrix Total 1.00 Netflix Vail Chipotle Starbucks 0.17 0.68 -0.17 0.32 Netflix 0.17 0.00112 -0.00008 -0.00007 0.00007 Vail 0.68 -0.00008 0.00130 0.00004 0.00006 Chipotle Starbucks -0.17 0.32 -0.00007 0.00007 0.00004 0.00006 0.00024 -0.00013 -0.00013 0.00031 Portfolio Variance Std Return 0.00274 0.05232 3% Standard Deviation Minimum Variance Frontier Portfolio 1 2 8% 7% Return 1% 2% 3% 4% 6% 7% 3 4 5 6 6% 5% 4% 3% 3. Calculate the minimum variance frontier for return increments 1%-7%. Report the variance of each. (hint: when you calculated the minimum variance you did so unconstrained. Now you will need to constrain returns to be a certain value) 4. Calculate the optimal portfolio for an investor with risk aversion parameter A=4 and A=64. Report the utility of each. 5. Now add a new asset called Rifi that offers 0% return and has 0% standard deviation of returns and is uncorrelated with other assets. (what should the covariance matrix row/column look like for this new asset). For the A=64 investor, what is the new optimal risk and return if they can include Rifi as part of their portfolio