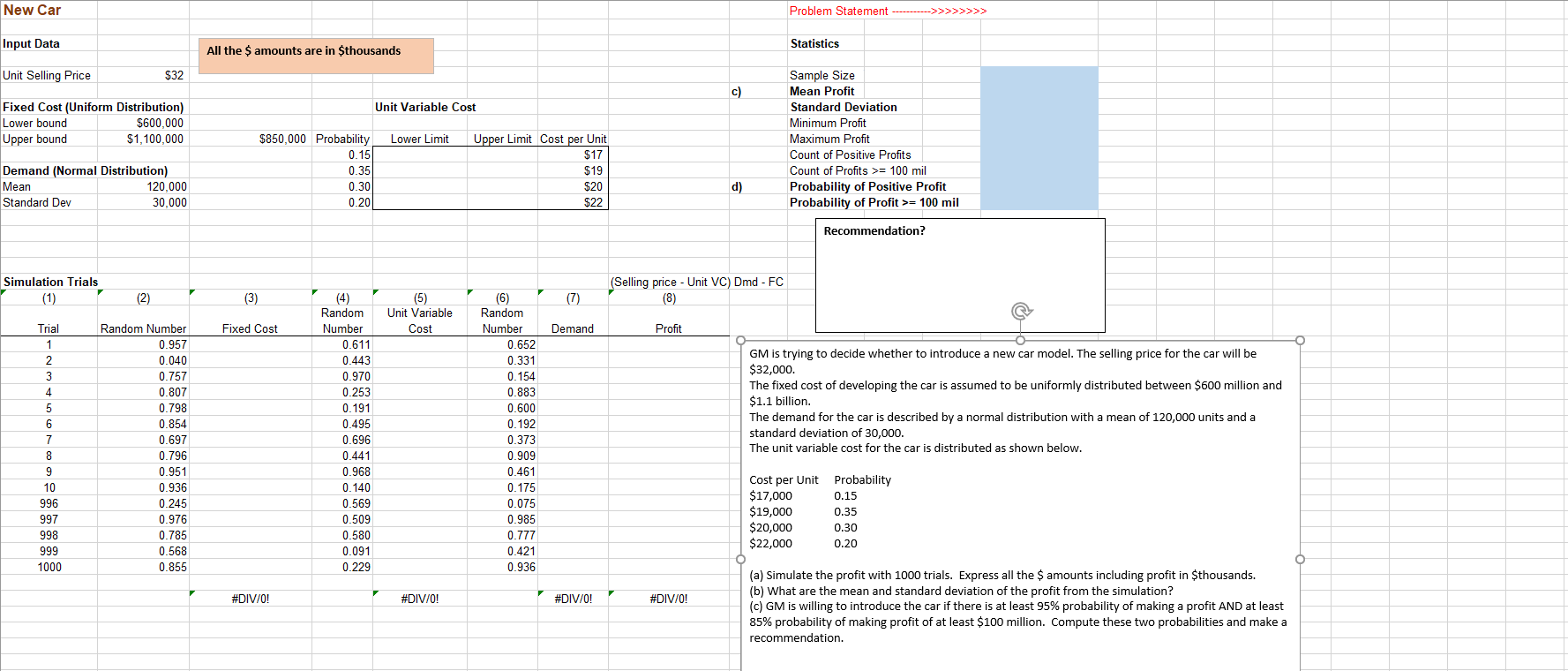
Question: New Car Problem Statement --------- ->>>>>>>> Input Data Statistics All the $ amounts are in $thousands Unit Selling Price $32 c) Unit Variable Cost Fixed
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


