no actual code needed, just the logic and analysis behind the algorithm

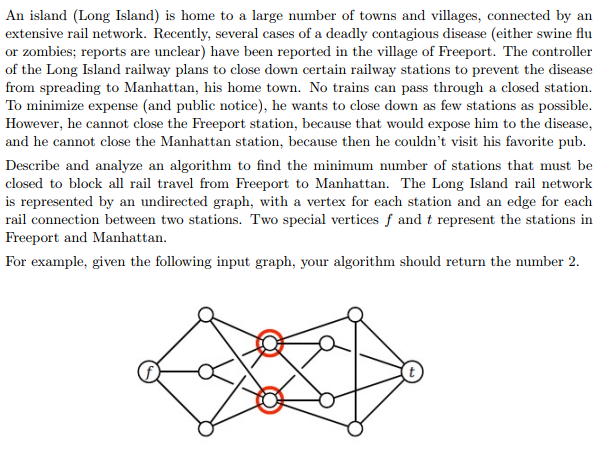
An island (Long Island) is home to a large number of towns and villages, connected by an extensive rail network. Recently, several cases of a deadly contagious disease (either swine flu or zombies; reports are unclear) have been reported in the village of Freeport. The controller of the Long Island railway plans to close down certain railway stations to prevent the disease from spreading to Manhattan, his home town. No trains can pass through a closed station. To minimize expense (and public notice), he wants to close down as few stations as possible However, he cannot close the Freeport station, because that would expose him to the disease and he cannot close the Manhattan station, because then he couldn't visit his favorite pub. Describe and analyze an algorithm to find the minimum number of stations that must be closed to block all rail travel from Freeport to Manhattan. The Long Island rail network is represented by an undirected graph, with a vertex for each station and an edge for each rail connection between two stations. Two special vertices f and t represent the stations in Freeport and Manhattan. For example, given the following input graph, your algorithm should return the number 2 An island (Long Island) is home to a large number of towns and villages, connected by an extensive rail network. Recently, several cases of a deadly contagious disease (either swine flu or zombies; reports are unclear) have been reported in the village of Freeport. The controller of the Long Island railway plans to close down certain railway stations to prevent the disease from spreading to Manhattan, his home town. No trains can pass through a closed station. To minimize expense (and public notice), he wants to close down as few stations as possible However, he cannot close the Freeport station, because that would expose him to the disease and he cannot close the Manhattan station, because then he couldn't visit his favorite pub. Describe and analyze an algorithm to find the minimum number of stations that must be closed to block all rail travel from Freeport to Manhattan. The Long Island rail network is represented by an undirected graph, with a vertex for each station and an edge for each rail connection between two stations. Two special vertices f and t represent the stations in Freeport and Manhattan. For example, given the following input graph, your algorithm should return the number 2