Non-probability sampling:

a. includes stratified sampling.

b. denies the researcher the use of statistical theory to estimate the probability of correct inferences.

c. always produces samples that possess distorted characteristics relative to the population.

d. is always less desirable than probability sampling.

e. requires the manipulation of sampling frames.

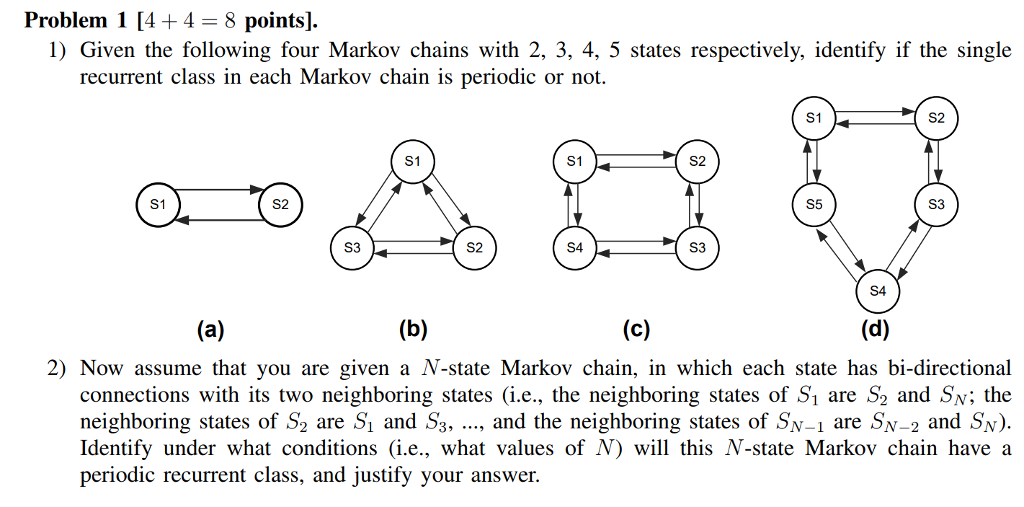
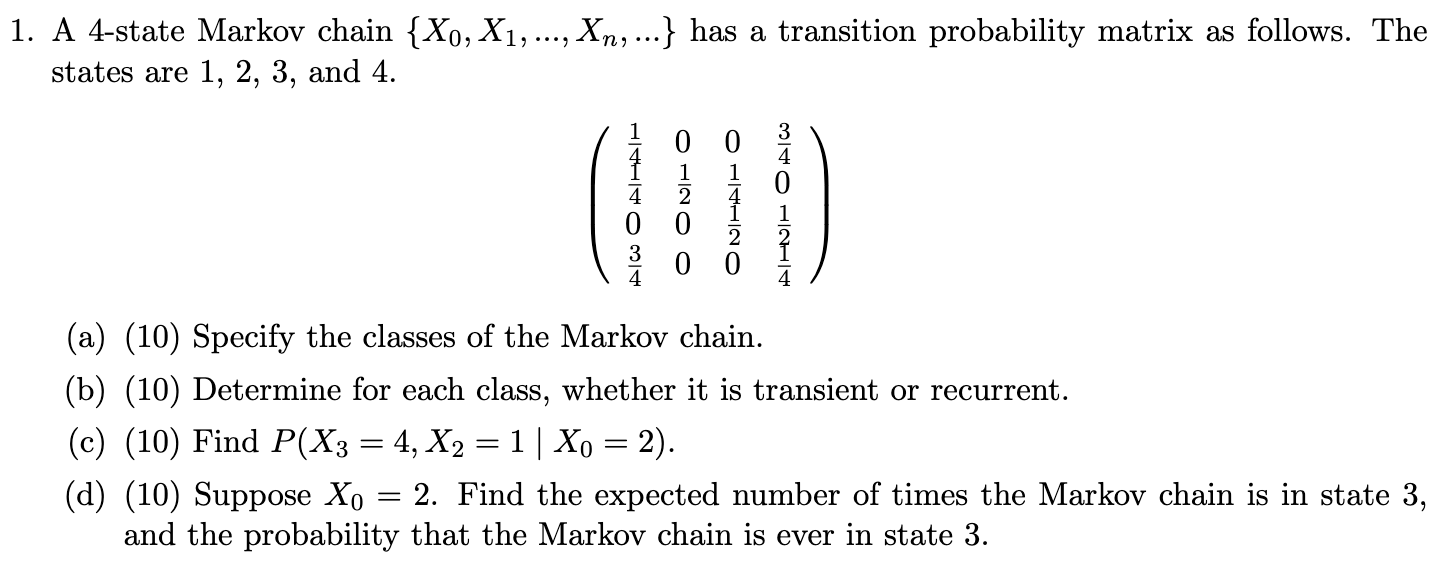
5. [12 marks] Consider the Markov chain with the following transition matrix. 0 0.5 0.5 0.5 0 0.5 0.5 0.5 0 (a) Draw the transition diagram of the Markov chain. (b) Is the Markov chain ergodic? Give a reason for your answer. (c) Compute the two step transition matrix of the Markov chain. (d) What is the state distribution #2 for t = 2 if the initial state distribution for t = 0 is no = (0.1, 0.5, 0.4) ?? (e) What is the average time /1,1 for the chain to return to state 1? Remember: Mij = 1+> Pikikj.Problem 1 [4 + 4 = 8 points]. 1) Given the following four Markov chains with 2, 3, 4, 5 states respectively, identify if the single recurrent class in each Markov chain is periodic or not. S1 S2 S1 S1 S2 S1 S2 $5 S3 S3 S2 $4 S3 S4 (a) (b) (c) (d) 2) Now assume that you are given a /V-state Markov chain, in which each state has bi-directional connections with its two neighboring states (i.e., the neighboring states of S, are S2 and Sy; the neighboring states of S2 are S, and S3, ..., and the neighboring states of SN_1 are SN-2 and SN). Identify under what conditions (i.e., what values of N) will this N-state Markov chain have a periodic recurrent class, and justify your answer.1. A 4-state Markov chain {Xo, X1, ..., Xn, ...} has a transition probability matrix as follows. The states are 1, 2, 3, and 4. ONHAIH O O ONHO PIANIH OPIC (a) (10) Specify the classes of the Markov chain. (b) (10) Determine for each class, whether it is transient or recurrent. (c) (10) Find P(X3 = 4, X2 = 1 | Xo = 2). (d) (10) Suppose Xo = 2. Find the expected number of times the Markov chain is in state 3, and the probability that the Markov chain is ever in state 3