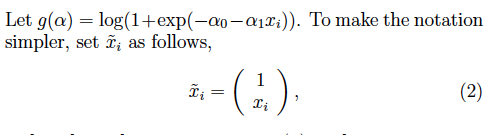
NOTE: For (d), f(x) and g(x) are two general convex functions.

Consider the log-likelihood for the single covariate (i.e. each 2; ER) logistic regression: log L(a) = (1-yi)(-00 - Q121) - log(1+exp(-00 - 21x:)) i=1 (1) Let g(a) = log(1+exp(-00-Q1.2)). To make the notation simpler, set i as follows, 11 #+(3), (c) Let v ER". Thinking of v as a column vector, define the matrix A = vul. Show that A is positive semidefinite, meaning that xAx > 0 for all x ER". (Hint: Consider (x+y)(v7x)). Use this fact to show that the function g(x) is convex. (d) Show the following facts. You can prove them from the definition or just explain the intuition through a graph. i. If two functions f(x) and h(z) are convex then so is their sum f(2) + g(). g(x) ii. If a function f(x) is convex, then -f(x) is concave. Then, show that log L(a) is a concave function. Consider the log-likelihood for the single covariate (i.e. each 2; ER) logistic regression: log L(a) = (1-yi)(-00 - Q121) - log(1+exp(-00 - 21x:)) i=1 (1) Let g(a) = log(1+exp(-00-Q1.2)). To make the notation simpler, set i as follows, 11 #+(3), (c) Let v ER". Thinking of v as a column vector, define the matrix A = vul. Show that A is positive semidefinite, meaning that xAx > 0 for all x ER". (Hint: Consider (x+y)(v7x)). Use this fact to show that the function g(x) is convex. (d) Show the following facts. You can prove them from the definition or just explain the intuition through a graph. i. If two functions f(x) and h(z) are convex then so is their sum f(2) + g(). g(x) ii. If a function f(x) is convex, then -f(x) is concave. Then, show that log L(a) is a concave function