NOTE THAT IS THE SAME QUESTION BUT DIFFERENT PARTS TO IT

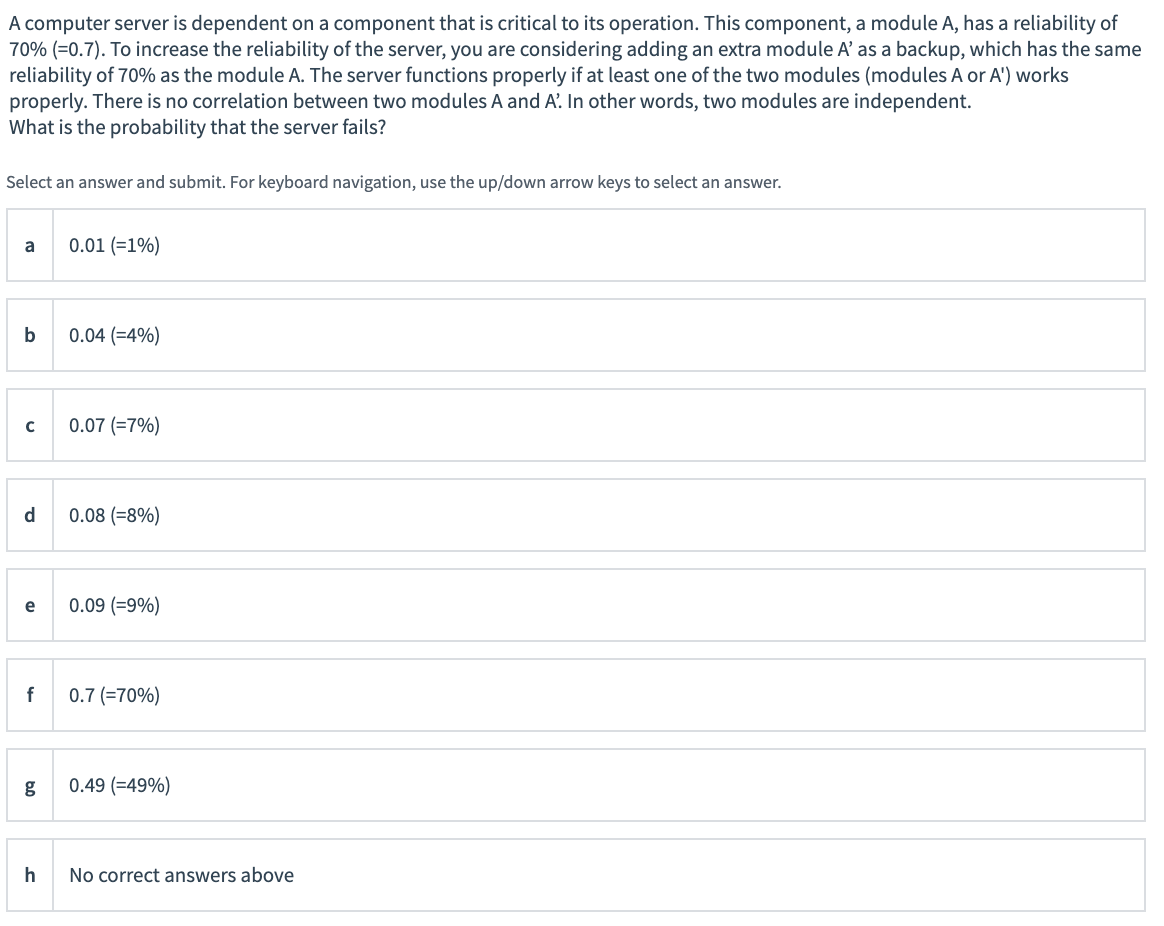
A computer server is dependent on a component that is critical to its operation. This component, a module A, has a reliability of 70% (=0.7). To increase the reliability of the server, you are considering adding an extra module A'as a backup, which has the same reliability of 70% as the module A. The server functions properly if at least one of the two modules (modules A or A') works properly. There is no correlation between two modules A and A? In other words, two modules are independent. What is the probability that the server fails? Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer. a 0.01 (=1%) b 0.04 (=4%) 0.07 (57%) d 0.08 (=8%) e 0.09 (59%) f 0.7 (=70%) g 0.49 (=49%) h No correct answers above This is a continuation from the previous question. What is the reliability of the server? Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer. a 0.01 (=1%) b 0.09 (=9%) 0.3 (=30%) d 0.64 (=64%) e 0.84 (=84%) f 0.91 (=91%) g 0.99 (=99%) h No correct answers above This is a continuation from the previous question. We currently have one backup module A' (and thus, there are two modules, A and A', in the system). Consider adding one more backup module A", which has the same reliability as A and A. However, this newly added backup module A" is perfectly positively correlated with the module A'. (Note that A and A' remain completely independent from each other with no correlation as before.) Which description about the reliability is true? Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer. The reliability of the system is beyond 100%. b The reliability of the system is exactly 100%. The reliability of the system is exactly 91% d The reliability of the system is exactly 70%. e The reliability of the system is less than 70%. f No answer above is correct