Question: Note that when the constant in the denominator is not 1 , we still can use the geometric series, but we have to multiply by
Note that when the constant in the denominator is not we still can use the geometric series, but we have to multiply by a form of that helps us We'll use
And now we can use the geometric series expression to get
Use differentiation andor integration to express the following function as a power series centered at
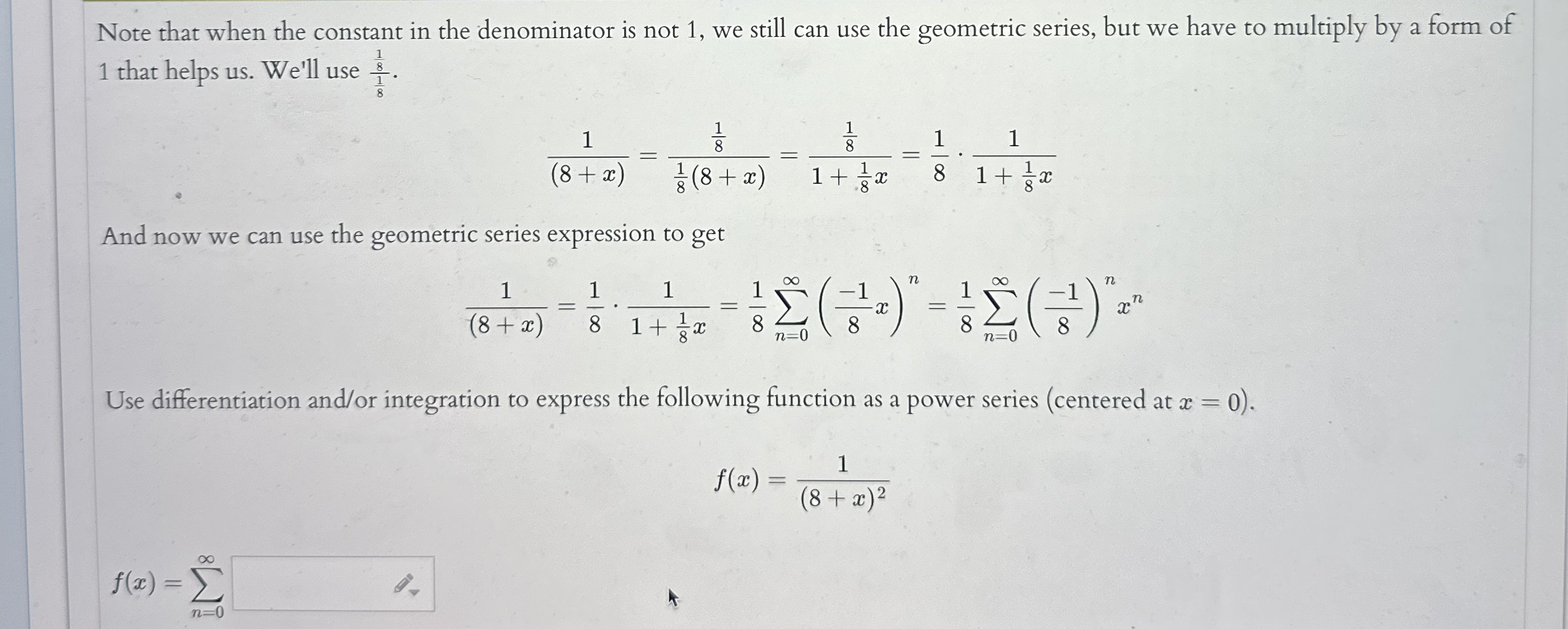
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


