NOTE:

This question requires R-Studio

For the data used in this question:

- PM2.5 (in micrograms per cubic metre): The PM2.5 concentration is a measure of air pollution. More precisely it is the concentration in the air of particles which are less than 2.5 micrometres in diameter.

- Dewpoint (in degrees Celsius): The dew point is the temperature to which the air must be cooled to become saturated with water vapour.

- Humidity (in percentage points): A measure of the amount of water vapour in the air.

- SE: A dummy variable equal to 1 if the wind comes from the south east and 0 otherwise

- NE: A dummy variable equal to 1 if the wind comes from the north east and 0 otherwise

- NW: A dummy variable equal to 1 if the wind comes from the north west and 0 otherwise

- Windspeed (in km/h): Measures the strength of the wind. Note: When the three wind direction dummies equal 0 the wind is calm or variable.

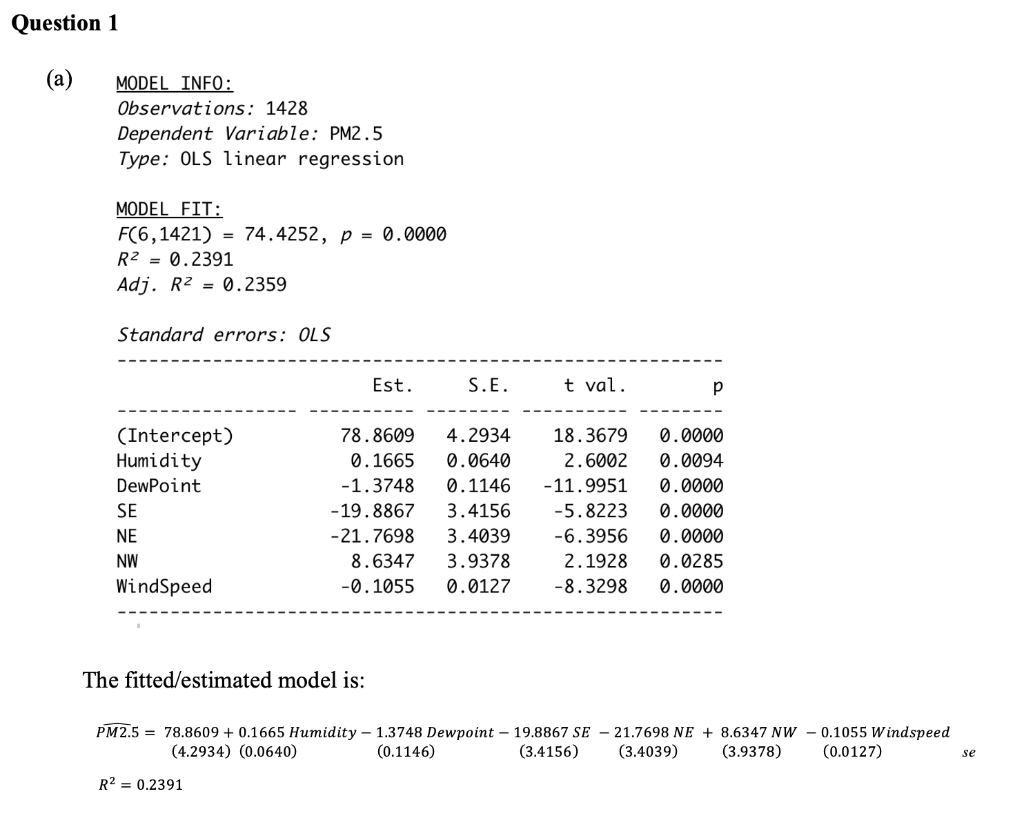
Model from Question 1 (a):

Question 3 (8 Marks)

(a) Starting from the model in Question 1 (a), you suspect that the change in PM2.5 concentration associated with an increase in windspeed of 1 km/h depends on the level of humidity. Extend the model in Question 1 to allow for this relationship. Write down the model, estimate this model and include your R result. (3 Marks)

(b) For your model in question 3(a), find and interpret the marginal effect of windspeed when humidity is (i) 40 percentage point, and (ii) 70 percentage point. Compare and comment on whether the marginal effect of windspeed on pm2.5 increase or decrease with humidity. (5 Marks)

MODEL INF0: Observations: 1428 Dependent Variable: PM2.5 Type: OLS linear regression MODELFIT:F(6,1421)=74.4252,p=0.0000R2=0.2391Adj.R2=0.2359 Standard errors: OLS The fitted/estimated model is: R2=0.2391 MODEL INF0: Observations: 1428 Dependent Variable: PM2.5 Type: OLS linear regression MODELFIT:F(6,1421)=74.4252,p=0.0000R2=0.2391Adj.R2=0.2359 Standard errors: OLS The fitted/estimated model is: R2=0.2391