[NP-completeness]

For a graph G = (V,E), an independent set is a set of vertices V such that for all (u,v) E, at most one of u or v is in 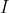. In other words, every edge has at most one end in 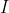. A vertex cover is a set of vertices S V if for every edge (u,v) E, at least one of u or v is in S. In other words, every edge has at least one end in S. Consider the following two problems:

Problem Vertex-Cover Input: G = (V,E), k Question: Does G contain a vertex cover S of size |S| k?

Problem: Independent-Set Input: G = (V,E), k Question: Does G contain an independent set 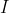of size | 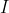| k?

(a) Show that Independent-Set P Vertex-Cover. (b) Show that Vertex-Cover P Independent-Set.