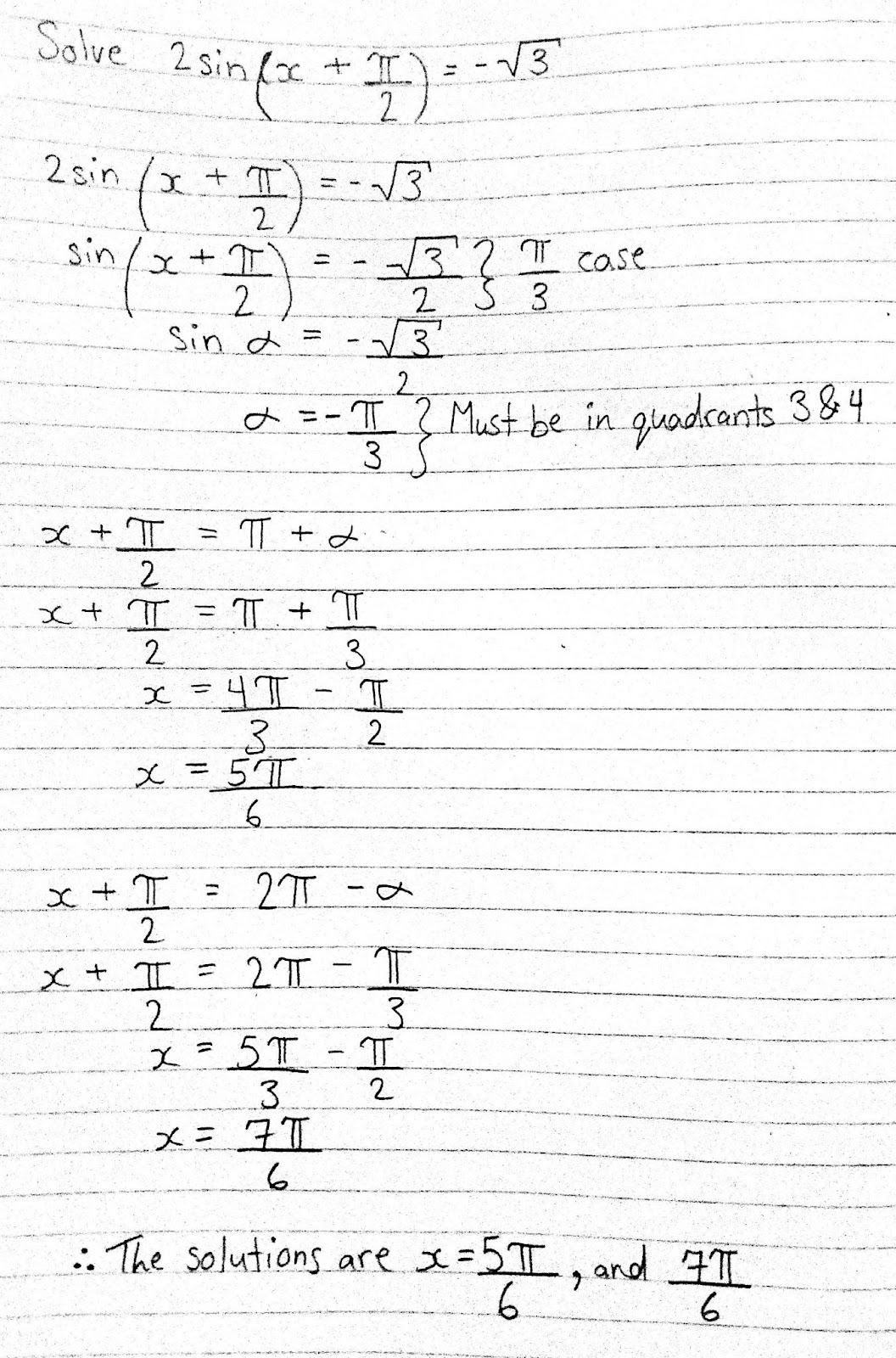NSTRUCTIONS: PLEASE READ BEFORE YOU BEGIN

Below are sample answers provided by my friends. Your task is to follow a similar structure and format, but make sure to modify the examples, graphs, and wording. Your goal is to create a visually appealing document. Please refrain from copying any examples verbatim.

Instructions:

• Change the wording and phrasing to enhance clarity and readability.
• Modify the format and layout for improved presentation.
• For the handwritten section, provide an example and write it manually.

Remember, the objective is to deliver a document that closely resembles the example below, but without directly copying any of its content.

Here is my friends answer :

As alluded to earlier. trigonometric functions innitely repeat themselves. This is why a trigonometric I equation can have innite solutions. Since it is impossible to define infinity, trigonometric equations have restrictions so that there can only be a finite number of solutions. Often, the restriction is written in an interval, such as CI 1: x 5 211: but not always. Let's analyze the steps to solving trigonometric equations through an example: Solve 2sin{x + %}= ~.,I'.wherelilI :1 x 5 2n ' Step 1: Start with the equation 2sin{x + %}i = 1.3 Step 2: Isolate for sinfx + %} TIE Step 3: Substitute [:2 {x + 7] Step 4: If it is a special case. then use what you ltnow about the special triangles to determine its exact ratio. Step 5: Use CAST to determine if this will be a positive or negative value. Step 6: Set a = (x + %}. and substitute the value you got from the earlier step for a Step T: Use order of operations to determine the value of I Step 3: Keep finding the other possible solutions for x that t with the interval restriction. What about quadratic trigonometric equations? Solving a quadratic trigonometric equation bears a striking resemblance to solving both a linear equation and a quadratic polynomial equation. It begins with factoring the equation, and then setting each factor equal to zero to solve for the value of theta. It requires the same steps as solving other trigonometric equations once each factor is set to zero. For example, solve 4sinx cosx + Ecosx - 2sinx -1 = t}. where U 1: x 1: 2n \f\f